Logistic Regression
Here, you might want to know how much mathematics is included in logistic regression
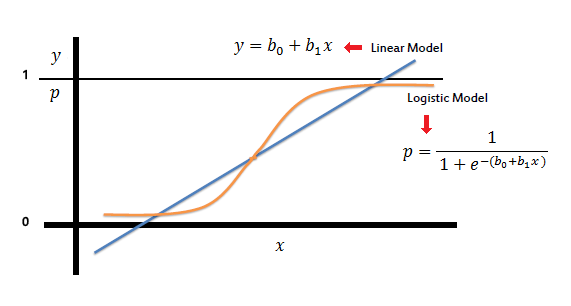
Let’s just take the most basic machine learning classification method - Logistic Regression for example. You may be very familier with it if you are assigned to solve an easy binary classification problem. Given a dataset heading like this, what would you do?
| id | Height(cm) | Weight(kg) | Gender |
|---|---|---|---|
| 1 | 180 | 83 | Male |
| 2 | 160 | 45 | Female |
| 3 | 176 | 76 | Male |
| 4 | 162 | 54 | Female |
| 5 | 157 | 43 | Female |
Obviously, we classify people that are taller and heavier as “Male”. So, we try to teach the machine to do this, either.
Programming
If you are a Python guy, you definitely will write:
from sklearn.linear_model import LogisticRegression
logmodel = LogisticRegression()
logmodel.fit(X_train,y_train) # Suppose we have splited the data into traing, test set.
predictions = logmodel.predict(X_test)
from sklearn.metrics import confusion_matrix
confusion_matrix(y_test,predictions)
If you are familier with R, you maybe write:
glm.fit <- glm(Gender ~ Height + Weight, data = data, family = binomial)
glm.probs <- predict(glm.fit,type = "response")
glm.pred <- ifelse(glm.probs > 0.5, "Male", "Female")
attach(data)
table(glm.pred,Gender) # confusion matrix
mean(glm.pred == Gender) # classification accuracy
I seems that just 3 or 4 lines of code will give you want you want. You do not see any mathematical elements in each case, right? That’s why we should thank the Python & R package developers.
Now, let us taste the version using plain Python without machine learning packages from Kaggle.
# prepare the data
import numpy as np
X = np.c_[np.ones((X.shape[0], 1)), X]
y = y[:, np.newaxis]
theta = np.zeros((X.shape[1], 1))
# 1. Sigmoid function --> core of logistic regression
def sigmoid(X, weight):
z = np.dot(X, weight)
return 1 / (1 + np.exp(-z))
# 2. loss function --> here comes the mathematics!
def loss(h, y):
return (-y * np.log(h) - (1 - y) * np.log(1 - h)).mean()
# 3. gradient descent, you definitely heard about it!
def gradient_descent(X, h, y):
return np.dot(X.T, (h - y)) / y.shape[0]
def update_weight_loss(weight, learning_rate, gradient):
return weight - learning_rate * gradient
# 4. Maximum Likelihood Estimation --> all mathematics
def log_likelihood(x, y, weights):
z = np.dot(x, weights)
ll = np.sum( y*z - np.log(1 + np.exp(z)) )
return ll
def gradient_ascent(X, h, y):
return np.dot(X.T, y - h)
def update_weight_mle(weight, learning_rate, gradient):
return weight + learning_rate * gradient
# 5. Now, it is time to train our model!
num_iter = 100000
intercept = np.ones((X.shape[0], 1))
X = np.concatenate((intercept, X), axis=1)
theta = np.zeros(X.shape[1])
for i in range(num_iter):
h = sigmoid(X, theta)
gradient = gradient_descent(X, h, y)
theta = update_weight_loss(theta, 0.1, gradient)
result = sigmoid(X, theta)
# 6. interpret the result
f = pd.DataFrame(np.around(result, decimals=6)).join(y)
f['pred'] = f[0].apply(lambda x : 0 if x < 0.5 else 1)
print("Accuracy (Loss minimization):")
f.loc[f['pred']==f['class']].shape[0] / f.shape[0] * 100
I am not saying we should go back to where we start. A lot of machine learning algorithms are stored in Sckit-learn within Python, which provides us great flexibility to solve ML problems!
However, we should understand each method to develop and utilize it into real applications.
It is your turn!
I have some questions for you:
-
Why we use logistic regression, not linear regression? What are the disadvantages of linear regression for classification?
-
What type of datasets is most suited for logistic regression?
-
Can you explain or interpret the hypothesis output of logistic regression?
-
Why we define the sigmoid function, create a new version of cost function, and applied MLE to derive logistic regression?
-
How to deal with overfitting?
-
What are the disadvantage of logistic regression?
My answers:
-
-
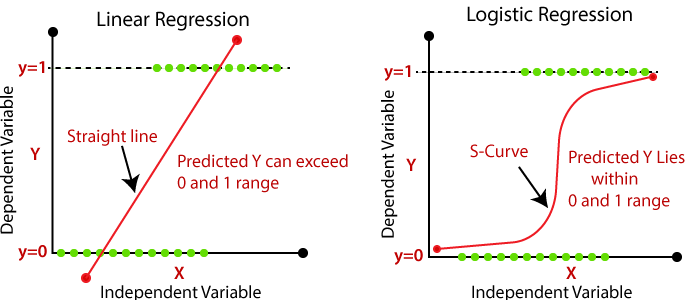
Linear regression can give us the values which are not between 0 and 1.
-
Also, linear regression is sensitive to the outliers. However, the sigmoid function restrict the values between 0 and 1, which can be interpreted as the conditional probability of assigning the data to the particular class given the data parametrized by theta.
-
-
-
Logistic regression likes overlapping data, instead of well separated data.
-
Linear Discriminent Analysis will perform better for well separated data since the decision boundary is linear.
-
-
-
We try to set a threshold to determine which class each data point should be assigned based on the conditional probability (I have clarified in Q1) derived from the sigmoid function.
-
Typically, we set the threshold to be 0.5. However, it can be adjusted between 0 and 1 for personal specification, such as restriction on TPR (True Positive Rate).
-
-
-
Sigmoid function helps transform the linear esitimation into non-linear one.
-
If we use the mean squared error as the cost function the same as linear regression, it is impossible to find the derivatives of the cost function with respect to theta, since the sigmoid function will make the cost function non-convex. So, we have to use gradient descent to minimize the cost function instead of computing the gradient by hand.
-
You might wonder why the cost function of logistic regression is like this! That is beacuse we applied the MLE to maximize the probability to make the model the most plausible for all data points. You always minimize the loss function, which is just the negative form of the loglikelihood after MLE.
-
-
-
It can be pretty easy for every machine learning method to be overfitting. It is not a big deal!
-
A regularization term is added to the cost function where the first part is loss function, and the second is the penalty term.

-
-
-
You should use k-fold cross validation to determine the highest polynomial of the features if the decision boundary is non-linear. It can be easy for this to overfit.
-
Logistic regression is unstable when dealing with well separated datasets.
-
Logistic regression requires relatively large datasets for training.
-
Logistic regression is not that popular for multiclassification problems. Sigmoid function should be ungraded to Softmax function(You may hear about it if you know about Neural Networks).
-
Conclusion
Mathematics and coding are just like twins that Nobody is able to completly separate if you want to be an expert in machine learning.
So, let this be a reminder for us all to always remember that it is extremely important and necessary to truly understand the mathematical backgroud of every machine learning algorithm as much as possible.
Enjoy Machine Learning!