KNN

Key takeaways

1. KNN is a simple yet effective machine learning algorithm used for both classification and regression tasks. It is a non-parametric method, meaning it does not make any assumptions about the underlying data distribution.

2. The algorithm works by finding the K nearest neighbors to a given data point based on a distance metric (e.g., Euclidean distance) and assigning a label or predicting a value based on the majority vote or average of the labels/values of its neighbors.

3. KNN is a lazy learning algorithm, which means it does not involve a training phase. Instead, during the prediction phase, it calculates the distances between the new data point and all existing data points in the training set.

4. The choice of the value of K in KNN is critical. A small K value can make the algorithm more sensitive to noise and outliers, while a large K value can lead to oversmoothing and loss of local patterns. The optimal value of K is often determined through cross-validation.

5. KNN can handle both numerical and categorical data. However, it requires the data to be preprocessed and normalized because the algorithm relies on the distance metric, which can be influenced by the scales and units of the features.

6. KNN does not provide explicit rules or feature importance. It considers all features equally and assumes that the features contributing to the decision are locally correlated with the target variable.

7. KNN is computationally expensive, especially for large datasets. Since it calculates the distances for every data point in the training set, the prediction time can be slow. Various techniques, such as KD-trees or ball trees, can be used to speed up the search process.

8. KNN is sensitive to the curse of dimensionality. As the number of features or dimensions increases, the algorithm may struggle to find meaningful neighbors because the distances between points tend to converge. Dimensionality reduction techniques or feature selection can help mitigate this issue.

9. KNN is a versatile algorithm that can be used for various applications such as recommendation systems, image recognition, anomaly detection, and more. It can also be used as a baseline model for benchmarking other complex algorithms.

10. KNN is a relatively interpretable algorithm. Since it relies on the concept of nearest neighbors, it can provide insights into the decision-making process by examining the neighbors and their characteristics.

Interview Questions

1. Explain the K-Nearest Neighbors (KNN) algorithm and how it works.

2. What is the role of K in KNN? How do you choose an optimal value for K?

3. What distance metrics can be used in KNN? Explain the difference between Euclidean distance and Manhattan distance.

4. How does KNN handle categorical data? Can it be used for feature selection?

5. What are the advantages and disadvantages of using KNN?

6. How does KNN deal with imbalanced datasets? Are there any techniques to address this issue?

7. Can KNN handle missing data? How would you handle missing values when using KNN?

8. How does KNN handle the curse of dimensionality? What techniques can be used to address this problem?

9. What are the differences between KNN classification and KNN regression? How are the predictions made in each case?

10. How would you evaluate the performance of a KNN model? What metrics can be used?

11. Can KNN be used for outlier detection? If yes, how?

12. What is the impact of scaling and normalization on KNN? Should you always preprocess the data before applying KNN?

13. What are some techniques to speed up the prediction phase of KNN for large datasets?

14. Can KNN handle streaming data or incremental learning? Explain your answer.

15. How does the presence of irrelevant features affect KNN performance? How can you address the issue of feature relevance?

16. What is the difference between instance-based learning and model-based learning? Which category does KNN fall into?

17. Can KNN be used for text classification? If yes, how would you represent text data for KNN?

18. How does the concept of cross-validation apply to KNN? Why is it important?

19. Are there any variations or extensions of KNN? Can you mention a few and explain their advantages?

20. How can you interpret the results of a KNN model? What insights can you gain from the nearest neighbors?

Solutions

Explain the K-Nearest Neighbors (KNN) algorithm and how it works:

The K-Nearest Neighbors (KNN) algorithm is a simple and versatile machine learning algorithm used for both classification and regression tasks. It operates based on the principle that data points that are close to each other are likely to belong to the same class or exhibit similar properties.

Here's how the algorithm works:

1. Training Phase: During the training phase, KNN simply stores the labeled data points in memory.

2. Prediction Phase: When a new unlabeled data point is provided for prediction, the algorithm calculates the distances between that point and all the training data points. The most common distance metric used is the Euclidean distance, but other distance metrics can be used as well.

3. Nearest Neighbor Selection: The algorithm selects the K data points from the training set that are closest to the new data point based on the calculated distances. These data points are known as the "nearest neighbors."

4. Voting (Classification) or Averaging (Regression): For classification tasks, KNN assigns the class label that is most frequent among the K nearest neighbors. In the case of regression tasks, KNN predicts the average of the target variable values of the K nearest neighbors.

5. Output: The predicted class label or value is returned as the output of the algorithm.

What is the role of K in KNN? How do you choose an optimal value for K?

The value of K in KNN determines the number of neighbors that will be considered when making predictions. It is a critical parameter that can significantly affect the performance of the algorithm.

The role of K can be summarized as follows:

• For smaller values of K, the model becomes more sensitive to noise and outliers. It may lead to overfitting and poor generalization because the decision boundary can be excessively influenced by a few nearby points.

• For larger values of K, the model becomes more stable and less sensitive to individual data points. However, it may lose the ability to capture local patterns and variations in the data.

To choose an optimal value for K, a common approach is to perform model selection using techniques like cross-validation. The data is divided into training and validation sets, and different values of K are tested. The value of K that yields the best performance (e.g., highest accuracy or lowest error) on the validation set is selected as the optimal value.

What distance metrics can be used in KNN? Explain the difference between Euclidean distance and Manhattan distance.

1. In KNN, various distance metrics can be used to measure the similarity or dissimilarity between data points. Some common distance metrics include:

   1. Euclidean Distance: Euclidean distance is the most widely used distance metric in KNN. It calculates the straight-line distance between two points in Euclidean space. For two points (p1, q1) and (p2, q2), the Euclidean distance is given by the formula:

      

      Euclidean distance considers the coordinates of the points as dimensions and calculates the shortest distance between them. It assumes that all dimensions are equally important and contributes to the overall distance equally.

   2. Manhattan Distance: Manhattan distance, also known as the city block distance or L1 norm, calculates the distance between two points by summing the absolute differences of their coordinates. For two points (p1, q1) and (p2, q2), the Manhattan distance is given by the formula:

      

      Manhattan distance gets its name from the idea of navigating through a city block, where you can only move along the grid-like streets. It measures the distance by summing the differences along each dimension, making right-angle turns. It is particularly useful when dealing with data that is constrained to move along orthogonal axes.

   The main difference between Euclidean distance and Manhattan distance lies in how they measure distance. Euclidean distance calculates the shortest straight-line distance between two points, treating their coordinates as dimensions. It captures the direct spatial relationship between points. On the other hand, Manhattan distance calculates the distance by summing the absolute differences along each dimension. It measures the "city block" distance, considering only horizontal and vertical movements. Manhattan distance is more suitable when movement is constrained to specific axes and right-angle turns are required.

   In KNN, the choice of distance metric depends on the nature of the data and the problem at hand. Other distance metrics, such as Minkowski distance, Mahalanobis distance, or cosine distance, can also be used based on specific requirements and data characteristics.

How does KNN handle categorical data? Can it be used for feature selection?

KNN can handle categorical data by using appropriate distance metrics that are suitable for categorical variables. One common approach is to use the Hamming distance or the simple matching distance, which count the number of mismatches or matches between two categorical feature vectors, respectively. These distance metrics treat categorical variables as binary variables, where a match is considered as 0 and a mismatch as 1.

To handle categorical data, the data preprocessing step involves converting categorical variables into numerical representations. This can be done through techniques like one-hot encoding, where each category is transformed into a binary feature. Once the categorical data is converted into numerical format, KNN can be applied in the same way as with numerical data.

Regarding feature selection, KNN itself does not inherently perform feature selection. However, you can use KNN as part of a feature selection process. One common approach is to use KNN to evaluate the performance of different subsets of features. By iteratively selecting subsets of features and evaluating the KNN performance, you can identify the subset that yields the best results. This process can help in feature selection by finding the most informative features for the given task.

What are the advantages and disadvantages of using KNN?

Advantages of using KNN:

• Simplicity: KNN is easy to understand and implement. It has a straightforward intuition and does not involve complex mathematical equations.

• Versatility: KNN can be used for both classification and regression tasks. It can handle various types of data, including numerical and categorical variables.

• No training phase: KNN is a lazy learning algorithm, meaning it does not require an explicit training phase. The model is built during the prediction phase, making it computationally efficient for training on large datasets.

• Interpretable: KNN provides interpretability as it allows you to examine the neighbors and their characteristics, helping to gain insights into the decision-making process.

Disadvantages of using KNN:

• Computational complexity: KNN can be computationally expensive, especially when dealing with large datasets. As the size of the training set increases, the prediction time also increases since distances need to be calculated for every training point.

• Sensitivity to feature scaling: KNN relies on distance metrics, and the choice of distance can be sensitive to the scales of the features. It is important to scale and normalize the features before applying KNN to avoid bias towards certain features.

• Determining the optimal K value: The choice of the K parameter in KNN is crucial and needs to be determined carefully. An inappropriate value of K can lead to overfitting or underfitting. It often requires experimentation and model selection techniques to find the optimal K value.

• Imbalanced data: KNN can be biased towards the majority class in imbalanced datasets. The class distribution affects the nearest neighbors, and the majority class can dominate the prediction. Techniques such as weighted KNN or resampling methods can help mitigate this issue.

Overall, while KNN is a simple and effective algorithm, it is important to consider its computational complexity, sensitivity to scaling, and appropriate handling of categorical data and imbalanced datasets.

How does KNN deal with imbalanced datasets? Are there any techniques to address this issue?

KNN can be biased towards the majority class in imbalanced datasets because the majority class tends to dominate the nearest neighbors. To address this issue, several techniques can be applied:

• Weighted KNN: Assigning higher weights to the instances of the minority class can help balance the influence of different classes during the prediction phase. This ensures that the minority class has a stronger impact on the decision boundary.

• Resampling methods: Techniques such as oversampling the minority class (e.g., Random Oversampling, SMOTE) or undersampling the majority class (e.g., Random Undersampling, Cluster Centroids) can help balance the class distribution. These methods create synthetic samples or reduce the number of majority class samples to achieve a more balanced representation.

• Ensemble methods: Using ensemble techniques like Balanced Bagging or Balanced Random Forest can help improve the performance on imbalanced datasets. These methods combine multiple KNN models trained on different balanced subsets of the data, reducing the bias towards the majority class.

Can KNN handle missing data? How would you handle missing values when using KNN?

KNN does not handle missing data explicitly, and missing values can cause issues during the distance calculations. To handle missing values when using KNN, some common approaches include:

• Data imputation: Missing values can be replaced or imputed with estimated values. Common imputation techniques include mean imputation, median imputation, mode imputation, or more advanced methods like regression imputation or k-nearest neighbor imputation. After imputing the missing values, KNN can be applied to the imputed dataset.

• Distance weighting: Another approach is to modify the distance calculations to give less weight to missing values or assign them a specific value that reflects their absence. This ensures that missing values do not dominate the distance computations and allow KNN to work with incomplete data.

How does KNN handle the curse of dimensionality? What techniques can be used to address this problem?

The curse of dimensionality refers to the challenges that arise when working with high-dimensional data. KNN can be affected by the curse of dimensionality because as the number of dimensions increases, the density of data points decreases, and distances tend to become less meaningful. To address this problem, some techniques can be employed:

• Dimensionality reduction: Techniques like Principal Component Analysis (PCA), Linear Discriminant Analysis (LDA), or t-SNE can be used to reduce the dimensionality of the data while preserving the most important information. These methods transform the data into a lower-dimensional space, reducing the impact of irrelevant or redundant features.

• Feature selection: Selecting a subset of relevant features can help mitigate the curse of dimensionality. Feature selection methods such as Recursive Feature Elimination (RFE), L1 regularization (Lasso), or information gain can be applied to identify the most informative features that contribute to the prediction.

• Manifold learning: Manifold learning techniques like Locally Linear Embedding (LLE), Isomap, or Laplacian Eigenmaps can help uncover the underlying low-dimensional structure of the data by preserving local relationships. These methods can reveal a more meaningful representation of the data, reducing the impact of high-dimensional noise.

What are the differences between KNN classification and KNN regression? How are the predictions made in each case?

The differences between KNN classification and KNN regression lie in the nature of the prediction task and the way predictions are made:

KNN Classification:

• Prediction Task: KNN classification is used for categorical or discrete prediction tasks, where the goal is to assign a class label to a new data point.

• Prediction Method: The prediction in KNN classification is made through majority voting. The class label that appears most frequently among the K nearest neighbors is assigned as the predicted class for the new data point. Each neighbor's class label contributes equally to the final decision.

• Output: The output of KNN classification is a class label or a categorical value.

KNN Regression:

• Prediction Task: KNN regression is used for continuous prediction tasks, where the goal is to predict a continuous or numeric value for a new data point.

• Prediction Method: The prediction in KNN regression is made through averaging. Instead of assigning a class label, the target values of the K nearest neighbors are averaged, and the resulting average is used as the predicted value for the new data point. The predicted value is a continuous value that represents the average of the target variable values of the neighbors.

• Output: The output of KNN regression is a continuous value or a numeric prediction.

In summary, KNN classification is used for categorical prediction tasks, and predictions are made through majority voting, while KNN regression is used for continuous prediction tasks, and predictions are made through averaging the target values of the nearest neighbors.

How would you evaluate the performance of a KNN model? What metrics can be used?

To evaluate the performance of a KNN model, several metrics can be used depending on the specific task:

• Accuracy: Accuracy measures the overall correctness of the predictions by calculating the ratio of correctly classified instances to the total number of instances. It is commonly used for balanced datasets.

• Precision, Recall, and F1-score: These metrics are useful for imbalanced datasets and binary classification tasks. Precision measures the proportion of correctly predicted positive instances, while recall measures the proportion of actual positive instances correctly predicted. F1-score is the harmonic mean of precision and recall, providing a balanced measure of performance.

• Confusion Matrix: A confusion matrix provides a detailed breakdown of the predicted versus actual class labels. It shows true positives, true negatives, false positives, and false negatives, allowing you to analyze the specific types of errors made by the KNN model.

• ROC Curve and AUC: ROC (Receiver Operating Characteristic) curve plots the true positive rate against the false positive rate at various classification thresholds. AUC (Area Under the Curve) summarizes the ROC curve's performance, providing a single-value measure of the model's discriminatory power.

The choice of evaluation metric depends on the specific problem, the class distribution, and the desired trade-offs between different types of errors.

Can KNN be used for outlier detection? If yes, how?

Yes, KNN can be used for outlier detection. The basic idea is that outliers are expected to have fewer neighboring data points compared to the majority of the data. The approach involves the following steps:

• Calculate the distance between each data point and its K nearest neighbors.

• Sort the distances in ascending order for each data point.

• Identify data points that have significantly larger distances compared to their neighbors. These data points can be considered outliers.

The choice of K is important as it determines the neighborhood size and affects the sensitivity of outlier detection. Smaller values of K make the algorithm more sensitive to outliers.

What is the impact of scaling and normalization on KNN? Should you always preprocess the data before applying KNN?

Scaling and normalization have a significant impact on KNN because the algorithm relies on distance calculations. If the features have different scales or units, those with larger values may dominate the distance computations, leading to biased results.

It is generally recommended to preprocess the data before applying KNN by scaling or normalizing the features. Common techniques include:

• Min-Max Scaling: Rescales the features to a specific range (e.g., [0, 1]) by subtracting the minimum value and dividing by the range.

• Standardization: Transforms the features to have zero mean and unit variance by subtracting the mean and dividing by the standard deviation.

• Other scaling methods: Additional scaling methods like Robust Scaling (using median and interquartile range) or Max Absolute Scaling (dividing by the maximum absolute value) may also be applicable depending on the data distribution and requirements.

Preprocessing the data helps to ensure that each feature contributes equally to the distance calculations and avoids biases due to different scales. However, it's worth noting that some distance metrics, such as Hamming distance for categorical variables, do not require scaling.

What are some techniques to speed up the prediction phase of KNN for large datasets?

For large datasets, the prediction phase of KNN can be computationally expensive due to distance calculations for each test instance. Here are some techniques to speed up the prediction phase:

1. Approximate Nearest Neighbor (ANN) Search: ANN algorithms, such as k-d trees, ball trees, or locality-sensitive hashing (LSH), can be used to index the training data and accelerate the search for nearest neighbors. These algorithms create efficient data structures that allow for faster neighbor retrieval, reducing the overall prediction time.

2. Dimensionality Reduction: Applying dimensionality reduction techniques, such as Principal Component Analysis (PCA) or t-SNE, can help reduce the number of features or compress the data while preserving most of the information. By working with a lower-dimensional representation, the number of distance calculations decreases, leading to faster predictions.

3. Nearest Neighbor Precomputation: If the dataset is static or changes infrequently, you can precompute the nearest neighbors for each training instance and store them. During the prediction phase, instead of recalculating the neighbors, you can directly retrieve them from the precomputed results, significantly reducing the computation time.

4. Parallelization: Utilize parallel processing techniques to distribute the distance calculations across multiple processors or machines. This can be achieved using parallel computing libraries or frameworks like multiprocessing or Spark. Parallelization can greatly speed up the prediction phase, especially for large-scale datasets.

5. Data Sampling: If the dataset is too large to handle efficiently, you can consider sampling a representative subset of the data. By selecting a smaller subset that maintains the distribution of the original data, you can reduce the computation time while preserving the overall characteristics of the dataset. However, be cautious as this may introduce a trade-off between computational efficiency and the accuracy of the predictions.

6. Algorithmic Optimization: Implementing efficient algorithms or data structures specifically designed for KNN can also help speed up the prediction phase. For example, using efficient distance calculation techniques, such as vectorized operations or optimized libraries, can improve the overall performance.

It's important to note that the choice of technique depends on the specific characteristics of the dataset, available computing resources, and the trade-offs between accuracy and computation time. It's recommended to experiment with different approaches and evaluate their impact on both speed and prediction quality.

Can KNN handle streaming data or incremental learning? Explain your answer.

KNN is not inherently designed for streaming data or incremental learning. Traditional KNN requires the entire training dataset to be present during the prediction phase because it calculates distances based on the complete set of training instances. This makes it impractical to update the model in real-time as new data arrives.

However, there are techniques that can be applied to adapt KNN for streaming data or incremental learning scenarios. One approach is to use approximate nearest neighbor algorithms, such as online or incremental KNN. These algorithms update the nearest neighbor structure as new data arrives, allowing for efficient and incremental updates to the model. Another approach is to use sliding window techniques, where a fixed-size window of the most recent data is maintained, and older data is discarded as new data arrives.

Overall, while KNN itself is not inherently suited for streaming data or incremental learning, with the use of appropriate adaptations and techniques, it is possible to make KNN work with streaming or incrementally arriving data.

what is streaming data?

Streaming data refers to a continuous and potentially infinite flow of data that arrives in real-time or near real-time. It is generated from various sources such as social media feeds, sensors, logs, financial transactions, IoT devices, and more. Streaming data is characterized by its high volume, velocity, and variability. Unlike static datasets, streaming data is continuously updated and often requires real-time processing and analysis.

Streaming data poses unique challenges due to its dynamic nature and the need for timely processing. Traditional batch processing techniques may not be suitable for handling streaming data as it arrives in a continuous and unbounded manner. Streaming data processing systems are designed to handle data in motion and provide real-time insights, allowing organizations to react quickly to changing conditions, identify patterns, detect anomalies, and make timely decisions based on up-to-date information.

Examples of applications that deal with streaming data include real-time analytics, fraud detection, recommendation systems, network monitoring, sensor data analysis, and social media sentiment analysis.

What is incremental learning?

Incremental learning, also known as online learning or lifelong learning, refers to a machine learning paradigm where a model learns from new data instances as they arrive in a sequential manner. Unlike traditional batch learning, which involves retraining the model on the entire dataset whenever new data is added, incremental learning enables the model to update its knowledge incrementally without discarding previously learned information.

In incremental learning, the model learns from each new data instance and incorporates it into its existing knowledge, adjusting its parameters or updating its internal representation accordingly. This allows the model to adapt and evolve over time as new data becomes available.

The advantages of incremental learning include:

1. Efficiency: Incremental learning avoids the need to retrain the model from scratch every time new data arrives, making it more computationally efficient, especially for large datasets.

2. Adaptability: The model can quickly adapt to changes in the data distribution or concept drift, as it continually learns from the most recent instances.

3. Scalability: Incremental learning enables handling large-scale datasets that may not fit entirely in memory, as it processes data instances one at a time or in small batches.

4. Real-time learning: With incremental learning, the model can update and improve its predictions in real-time, making it suitable for scenarios where immediate response or decision-making is required.

However, there are challenges in incremental learning, such as managing the trade-off between retaining previous knowledge and incorporating new information, handling concept drift, avoiding catastrophic forgetting, and ensuring model stability. Careful consideration of techniques like regularization, forgetting mechanisms, memory management, and model architecture design is necessary to maintain a good balance between stability and adaptability.

Incremental learning finds applications in domains where the data distribution changes over time or when new data arrives continuously, such as online recommendation systems, adaptive control systems, fraud detection, and personalized learning systems.

How does the presence of irrelevant features affect KNN performance? How can you address the issue of feature relevance?

The presence of irrelevant features can negatively impact KNN performance in several ways:

• Increased computation time: Irrelevant features contribute to the curse of dimensionality, making the distance calculations computationally expensive and less meaningful.

• Noise and misclassification: Irrelevant features may introduce noise into the similarity measurements, leading to less accurate neighbor selection and potentially misclassifying instances.

To address the issue of feature relevance in KNN, you can employ feature selection or dimensionality reduction techniques:

• Feature Selection: Selecting a subset of relevant features can improve KNN performance. Techniques such as Recursive Feature Elimination (RFE), L1 regularization (Lasso), or information gain can be applied to identify the most informative features that contribute to the prediction.

• Dimensionality Reduction: Techniques like Principal Component Analysis (PCA), Linear Discriminant Analysis (LDA), or t-SNE can be used to reduce the dimensionality of the data while preserving the most important information. These methods transform the data into a lower-dimensional space, filtering out irrelevant features and reducing the impact of noise.

By eliminating or reducing the influence of irrelevant features, you can improve the efficiency and accuracy of KNN predictions.

What is the difference between instance-based learning and model-based learning? Which category does KNN fall into?

• Instance-based Learning: Instance-based learning, also known as lazy learning, involves storing the training instances and making predictions based on the similarity or distance between the new instance and the stored instances. It does not explicitly build a generalized model during the training phase but relies on the stored instances for inference. KNN falls into this category, as it directly uses the training instances to make predictions.

• Model-based Learning: Model-based learning, also known as eager learning, involves constructing a generalized model from the training data during the training phase. The model represents a summary or abstraction of the data and is used for making predictions on new instances. Examples of model-based learning algorithms include decision trees, linear regression, and neural networks.

In summary, instance-based learning algorithms like KNN directly store and use the training instances for predictions, while model-based learning algorithms build a generalized model during training and use it for inference.

Can KNN be used for text classification? If yes, how would you represent text data for KNN?

Yes, KNN can be used for text classification. However, text data requires appropriate representation before it can be used with KNN. Two commonly used representations for text data in KNN are:

• Bag-of-Words (BoW): In the BoW representation, each document is represented as a vector, and the vector's dimensions correspond to the unique words in the entire corpus. The value in each dimension represents the frequency or presence/absence of the word in the document. This way, text data is transformed into numerical feature vectors that can be used with KNN.

• TF-IDF (Term Frequency-Inverse Document Frequency): TF-IDF is another representation that accounts for word frequency in a document as well as its relevance in the entire corpus. It assigns higher weights to words that appear frequently in a document but are rare in the corpus. TF-IDF transforms text data into numeric vectors similar to the BoW representation.

These representations capture the information present in the text documents and allow KNN to measure similarity or distance between documents for classification purposes.

How does the concept of cross-validation apply to KNN? Why is it important?

Cross-validation is a technique used to assess the performance and generalization ability of a machine learning model. It can be applied to KNN as well. The basic idea behind cross-validation is to partition the available data into multiple subsets, or folds, and iteratively use one fold as a validation set while training the model on the remaining folds.

For KNN, cross-validation helps in evaluating the model's performance by providing an estimate of how well it will generalize to unseen data. Since KNN relies on the proximity of data points, the choice of K and the distance metric can significantly affect the model's performance. Cross-validation allows you to tune these hyperparameters by comparing the model's performance on different folds and selecting the values that yield the best results.

Cross-validation helps in mitigating the risk of overfitting, where the model performs well on the training data but poorly on unseen data. It provides a more robust assessment of the model's capabilities and helps in selecting the most suitable hyperparameters for KNN.

Are there any variations or extensions of KNN? Can you mention a few and explain their advantages?

Yes, there are variations and extensions of KNN that address some of its limitations or incorporate additional techniques. Some examples include:

• Weighted KNN: In standard KNN, each neighbor has an equal vote in the prediction. Weighted KNN assigns weights to neighbors based on their proximity to the test instance. Closer neighbors have higher weights, indicating their stronger influence on the prediction.

• Radius-based KNN: Instead of considering a fixed number of nearest neighbors, radius-based KNN considers all neighbors within a specified radius. This approach is useful when the density of neighbors varies across the feature space.

• Kernel Density Estimation-based KNN: This variation combines KNN with kernel density estimation. It estimates the probability density function for each class in the feature space and assigns a class label based on the density of neighbors within a specified radius.

• Locality-Sensitive Hashing (LSH) for KNN: LSH is a technique that allows for efficient approximate nearest neighbor search. It uses hash functions to index the data, enabling fast retrieval of neighbors without exhaustively calculating distances.

These variations and extensions offer advantages such as improved flexibility, handling varying densities, incorporating weights, or providing faster neighbor search in high-dimensional spaces.

How can you interpret the results of a KNN model? What insights can you gain from the nearest neighbors?

Interpreting the results of a KNN model involves analyzing the nearest neighbors of a given instance to gain insights and understand the reasoning behind the model's prediction. Here are some ways to interpret the results and the insights you can gain from the nearest neighbors:

1. Class Distribution: By examining the class labels of the nearest neighbors, you can observe the distribution of classes. If the majority of the nearest neighbors belong to a specific class, it indicates that the prediction is influenced by instances with similar characteristics.

2. Decision Boundaries: The proximity of neighbors can provide insights into the decision boundaries of the model. By visualizing the nearest neighbors in relation to the predicted instance, you can understand how the model determines the boundaries between different classes.

3. Outlier Detection: If a predicted instance has nearest neighbors from different classes or distant neighbors, it suggests that the instance lies on the outskirts of the decision boundaries. This can be an indication of an ambiguous or outlier case.

4. Feature Importance: Examining the feature values of the nearest neighbors can help identify the important features that contribute to the prediction. Features that consistently differ between neighbors of different classes can be considered important for the decision-making process.

5. Similarity Patterns: By analyzing the attributes and characteristics of the nearest neighbors, you can identify patterns of similarity or dissimilarity. This can provide insights into the relationships between instances and help identify common traits or shared properties within classes.

6. Error Analysis: Investigating cases where the predicted class differs from the majority class of the nearest neighbors can help identify potential misclassifications or cases where the model struggles to generalize correctly. This analysis can guide further model improvements or data preprocessing steps.

Overall, interpreting the results of a KNN model involves understanding the relationships between instances, exploring decision boundaries, identifying important features, detecting outliers, and gaining insights into the reasoning behind the model's predictions. By analyzing the nearest neighbors, you can gain a deeper understanding of how the model operates and make informed decisions about the model's performance and potential areas for improvement.

Python Application

Using Sklearn

​x
24
1
from sklearn.datasets import load_iris
2
from sklearn.model_selection import train_test_split
3
from sklearn.neighbors import KNeighborsClassifier
4
from sklearn.metrics import accuracy_score
5

6
# Load the IRIS dataset
7
iris = load_iris()
8

9
# Split the data into training and testing sets
10
X_train, X_test, y_train, y_test = train_test_split(iris.data, iris.target, test_size=0.2, random_state=42)
11

12
# Create a KNN classifier object
13
knn = KNeighborsClassifier(n_neighbors=3)
14

15
# Train the classifier
16
knn.fit(X_train, y_train)
17

18
# Make predictions on the test set
19
y_pred = knn.predict(X_test)
20

21
# Calculate accuracy
22
accuracy = accuracy_score(y_test, y_pred)
23
print("Accuracy:", accuracy)

In this example, we first import the necessary modules: load_iris to load the IRIS dataset, train_test_split to split the data into training and testing sets, KNeighborsClassifier to create the KNN classifier, and accuracy_score to calculate the accuracy of the predictions.

Next, we load the IRIS dataset using load_iris(). We then split the dataset into training and testing sets using train_test_split(), where 80% of the data is used for training and 20% for testing.

We create a KNN classifier object knn with n_neighbors=3, indicating that the three nearest neighbors will be considered for classification.

The classifier is trained using the training data with knn.fit(X_train, y_train). Then, we make predictions on the test set using knn.predict(X_test) and store the predicted labels in y_pred.

Finally, we calculate the accuracy of the predictions by comparing the predicted labels y_pred with the true labels y_test and print the accuracy score.

This example demonstrates a basic implementation of a KNN classifier using the IRIS dataset. You can modify the code or explore additional functionalities of scikit-learn to further enhance the application.

KNeighborsClassifier()

xxxxxxxxxx
1
1
class sklearn.neighbors.KNeighborsClassifier(n_neighbors=5, weights='uniform', algorithm='auto', leaf_size=30, p=2, metric='minkowski', metric_params=None, n_jobs=None)

• n_neighbors：指定要考虑的最近邻居的数量，通常是一个正整数，默认为5。

• weights：指定如何对邻居的权重进行计算，默认为'uniform'，表示所有邻居的权重相等。其他可选值包括'distance'（权重与距离成反比）和用户自定义的可调用函数。

• algorithm：指定用于计算最近邻居的算法。可选值包括'auto'（自动选择合适的算法）、'ball_tree'（使用BallTree算法）、'kd_tree'（使用KDTree算法）和'brute'（使用暴力搜索）。默认为'auto'。

• leaf_size：指定BallTree或KDTree的叶子节点大小，默认为30。较小的值将导致构建树的速度更慢但查询速度更快。

• p：指定Minkowski距离度量的参数。当p=1时，使用曼哈顿距离；当p=2时，使用欧氏距离。默认为2。

• metric：指定用于计算距离的度量标准，默认为'minkowski'。还可以选择其他度量标准，如'euclidean'、'manhattan'等。

• metric_params：指定距离度量标准的额外参数。默认为None。

• n_jobs：指定并行计算的作业数量。默认为None，表示不使用并行计算。

KNeighborsClassifier的主要方法：

• fit(X, y)：用于训练模型，其中X是训练数据的特征向量，y是对应的目标变量。

• predict(X)：用训练好的模型对新的数据进行预测，返回预测的目标变量。

• predict_proba(X)：返回每个类别的概率估计。仅在KNeighborsClassifier的weights参数设置为'distance'时可用。

• kneighbors(X)：返回测试集中每个样本的最近邻居。可以获取最近邻居的距离和索引。

• score(X, y)：返回给定测试数据和标签的平均准确率。

KNeighborsClassifier的工作流程：

1. 初始化KNeighborsClassifier对象，并根据提供的参数设置模型的属性。

2. 使用fit(X, y)方法将训练数据X和对应的目标变量y传递给模型，以训练KNN分类器。模型会根据提供的数据建立一个存储训练样本的数据结构，以便后续的预测和计算最近邻居。

3. 当需要对新的样本进行分类时，使用predict(X)方法传递测试数据X给模型，返回预测的目标变量。KNN分类器会根据选择的最近邻居数量（n_neighbors）和距离度量（metric）来计算测试样本与训练样本之间的距离，然后根据最近邻居的标签进行投票或权重计算，确定预测结果。

4. 可以使用其他方法如predict_proba(X)返回每个类别的概率估计，或使用kneighbors(X)获取测试集中每个样本的最近邻居的距离和索引。

5. 使用score(X, y)方法可以评估模型的准确率，计算给定测试数据X和对应的真实标签y的平均准确率。

From Scratch

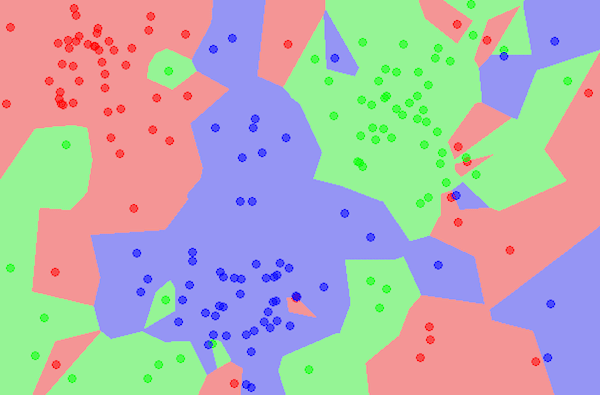
• Step 1: Calculate Euclidean Distance.

• Step 2: Get Nearest Neighbors.

• Step 3: Make Predictions.

xxxxxxxxxx
1
11
1
import numpy as np
2
from sklearn.datasets import load_iris
3
from sklearn.model_selection import train_test_split
4
from sklearn.metrics import accuracy_score
5

6
# Load the IRIS dataset
7
iris = load_iris()
8

9
# Split the data into training and testing sets
10
X_train, X_test, y_train, y_test = train_test_split(iris.data, iris.target, test_size=0.2, random_state=42)

首先，导入所需的库。使用load_iris函数加载IRIS数据集，然后使用train_test_split函数将数据集划分为训练集和测试集，其中测试集占比为20%。

xxxxxxxxxx
1
1
def euclidean_distance(x1, x2):
2
    return np.sqrt(np.sum((x1 - x2)**2))

定义一个计算欧氏距离的函数euclidean_distance，输入两个向量x1和x2，使用numpy的函数计算两个向量之间的差的平方和，然后取平方根作为欧氏距离。

xxxxxxxxxx
1
18
1
class KNN:
2
    def __init__(self, n_neighbors=3):
3
        self.n_neighbors = n_neighbors
4

5
    def fit(self, X, y):
6
        self.X_train = X
7
        self.y_train = y
8

9
    def predict(self, X):
10
        y_pred = []
11
        for sample in X:
12
            distances = [euclidean_distance(sample, x) for x in self.X_train]
13
            nearest_indices = np.argsort(distances)[:self.n_neighbors]
14
            nearest_labels = self.y_train[nearest_indices]
15
            counts = np.bincount(nearest_labels)
16
            y_pred.append(np.argmax(counts))
17
        return np.array(y_pred)

定义KNN类。在__init__方法中初始化最近邻居的数量n_neighbors。fit方法用于存储训练数据X和对应的目标变量y。predict方法用于对输入的测试数据X进行预测。对于每个测试样本，计算它与训练样本的距离，选择最近的n_neighbors个样本，进行多数投票并返回预测结果。

xxxxxxxxxx
1
1
knn = KNN(n_neighbors=3)
2

3
# Train the classifier
4
knn.fit(X_train, y_train)
5

6
# Make predictions on the test set
7
y_pred = knn.predict(X_test)

创建一个KNN对象knn，并指定最近邻居的数量为3。然后，使用训练集调用fit方法训练分类器。接下来，使用测试集调用predict方法进行预测，将预测结果存储在y_pred中。

xxxxxxxxxx
1
1
accuracy = accuracy_score(y_test, y_pred)
2
print("Accuracy:", accuracy)

计算预测结果的准确率。使用accuracy_score函数，将真实的目标变量y_test和预测的目标变量y_pred作为输入参数，计算准确率。最后打印准确率的结果。

xxxxxxxxxx
1
45
1
import numpy as np
2
from sklearn.datasets import load_iris
3
from sklearn.model_selection import train_test_split
4
from sklearn.metrics import accuracy_score
5

6
# Load the IRIS dataset
7
iris = load_iris()
8

9
# Split the data into training and testing sets
10
X_train, X_test, y_train, y_test = train_test_split(iris.data, iris.target, test_size=0.2, random_state=42)
11

12
def euclidean_distance(x1, x2):
13
    return np.sqrt(np.sum((x1 - x2)**2))
14

15
class KNN:
16
    def __init__(self, n_neighbors=3):
17
        self.n_neighbors = n_neighbors
18

19
    def fit(self, X, y):
20
        self.X_train = X
21
        self.y_train = y
22

23
    def predict(self, X):
24
        y_pred = []
25
        for sample in X:
26
            distances = [euclidean_distance(sample, x) for x in self.X_train]
27
            nearest_indices = np.argsort(distances)[:self.n_neighbors]
28
            nearest_labels = self.y_train[nearest_indices]
29
            counts = np.bincount(nearest_labels)
30
            y_pred.append(np.argmax(counts))
31
        return np.array(y_pred)
32

33
# Create KNN classifier object
34
knn = KNN(n_neighbors=3)
35

36
# Train the classifier
37
knn.fit(X_train, y_train)
38

39
# Make predictions on the test set
40
y_pred = knn.predict(X_test)
41

42
# Calculate accuracy
43
accuracy = accuracy_score(y_test, y_pred)
44
print("Accuracy:", accuracy)