SVM

Key takeaways

1. SVM is a supervised learning algorithm primarily used for binary classification, but it can also be extended to handle multi-class classification problems.

2. The goal of SVM is to find an optimal hyperplane that maximizes the margin between different classes of samples, aiming for better generalization.

3. SVM is based on the concept of support vectors, which are the samples closest to the hyperplane and determine its position.

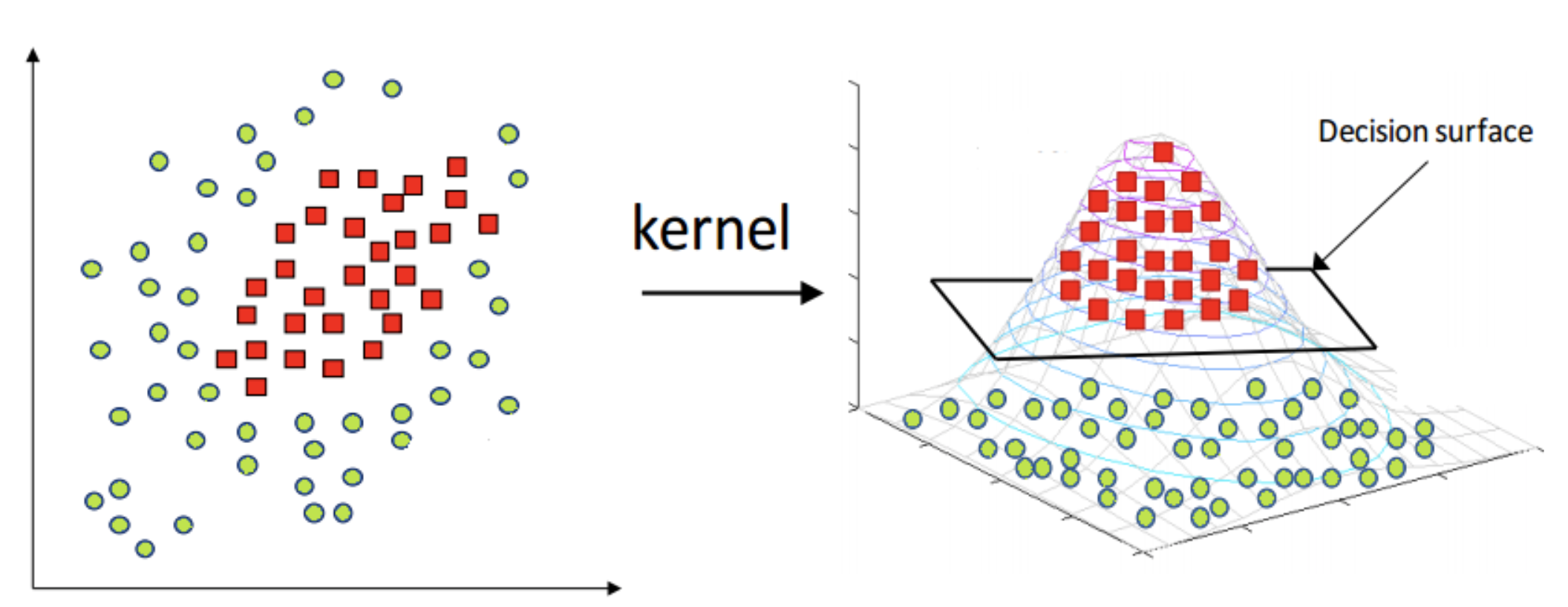
4. SVM can employ different kernel functions (e.g., linear, polynomial, Gaussian) to map nonlinear problems into a higher-dimensional feature space, where a linear hyperplane can be found.

5. SVM optimizes the model by minimizing the structural risk, which is composed of the empirical risk and a regularization term to control the model's complexity and fitting behavior.

6. The optimization problem of SVM can be solved using quadratic programming techniques, such as Sequential Minimal Optimization (SMO).

7. SVM performs well with small sample sizes and high-dimensional data, effectively handling cases where the number of features exceeds the number of samples.

8. SVM is relatively sensitive to outliers and noise since they can become support vectors and affect the position of the hyperplane.

9. SVM can be used for feature selection, where the weights of the support vectors can indicate the importance of features, allowing for feature screening.

10. SVM has widespread applications in various fields, including text classification, image recognition, bioinformatics, and more.

Interview Questions

1. What is Support Vector Machine (SVM)?

2. How does SVM differ from other machine learning algorithms?

3. What is the objective of SVM?

4. Explain the concept of hyperplane in SVM.

5. What is the kernel trick in SVM?

6. What are the advantages and disadvantages of SVM?

7. What is the difference between linear SVM and non-linear SVM?

8. How is the margin defined in SVM?

9. What is the purpose of the slack variable in SVM?

10. What is the role of the C parameter in SVM?

11. How do you handle imbalanced datasets in SVM?

12. How do you handle missing values in SVM?

13. Explain the process of SVM training.

14. What are support vectors in SVM?

15. How do you handle categorical variables in SVM?

16. What is the difference between hard margin and soft margin in SVM?

17. How do you choose the optimal hyperparameters in SVM?

18. Can SVM be used for multi-class classification? If yes, how?

19. What are the possible applications of SVM?

20. How does SVM handle outliers in the dataset?

Solutions

What is Support Vector Machine (SVM)?

Support Vector Machine (SVM) is a supervised machine learning algorithm used for classification and regression tasks. It finds a hyperplane in a high-dimensional feature space that optimally separates different classes or predicts the continuous values of the target variable.

How does SVM differ from other machine learning algorithms?

SVM differs from other machine learning algorithms in several ways:

• SVM focuses on finding the optimal hyperplane that maximizes the margin between classes, while other algorithms may focus on minimizing error or maximizing likelihood.

• SVM can handle high-dimensional data efficiently by using a subset of training samples called support vectors, which reduces computational complexity.

• SVM can handle both linear and non-linear decision boundaries through the use of kernel functions.

• SVM is less prone to overfitting, as it aims to maximize the margin between classes, leading to better generalization.

What is the objective of SVM?

The objective of SVM is to find the optimal hyperplane that separates the classes with the maximum margin. The margin is the distance between the hyperplane and the nearest data points of each class. By maximizing the margin, SVM aims to achieve better generalization and improve the classifier's ability to correctly classify new, unseen data.

Explain the concept of hyperplane in SVM.

In SVM, a hyperplane is a decision boundary that separates the input data points into different classes. For a binary classification problem, a hyperplane in a two-dimensional feature space is a line, while in higher-dimensional spaces, it becomes a hyperplane. The optimal hyperplane is the one that maximizes the margin between the classes, ensuring the greatest separation between the data points.

What is the kernel trick in SVM?

The kernel trick is a technique used in SVM to transform the input data into a higher-dimensional feature space without explicitly calculating the transformed features. It allows SVM to efficiently handle non-linear decision boundaries. The kernel function computes the similarity between two data points in the higher-dimensional space, making it possible to perform calculations as if they were in the original input space. Common kernel functions include the linear, polynomial, radial basis function (RBF), and sigmoid kernels.

What are the advantages and disadvantages of SVM?

Advantages of SVM:

• Effective in high-dimensional spaces and with a small number of training samples.

• Can handle both linear and non-linear decision boundaries using kernel functions.

• Less prone to overfitting due to the maximum margin principle.

• Can handle large feature spaces efficiently.

Disadvantages of SVM:

• Computationally intensive, especially with large datasets.

• Requires careful selection of kernel functions and tuning of hyperparameters.

• Doesn't directly provide probability estimates (though they can be approximated).

• Can be sensitive to the choice of parameters and the scaling of input features.

What is the difference between linear SVM and non-linear SVM?

Linear SVM assumes a linear decision boundary between classes, where the hyperplane is a straight line or a hyperplane in the feature space. It is suitable for linearly separable datasets.

Non-linear SVM uses kernel functions to transform the input space into a higher-dimensional feature space, where a linear hyperplane can effectively separate the classes. It is suitable for datasets that are not linearly separable, as it allows for complex decision boundaries.

How is the margin defined in SVM?

The margin in SVM is the perpendicular distance between the decision hyperplane and the nearest data points of each class. The objective of SVM is to find the hyperplane that maximizes this margin. A larger margin indicates better separation and potential for better generalization.

What is the purpose of the slack variable in SVM?

The slack variable in SVM allows for some misclassification or violation of the margin in order to handle non-linear

What is the role of the C parameter in SVM?

The C parameter in SVM controls the trade-off between achieving a wider margin and allowing for misclassifications. A smaller value of C allows for a wider margin and more misclassifications, while a larger value of C imposes a stricter margin and penalizes misclassifications more heavily. In other words, a smaller C value leads to a softer decision boundary, while a larger C value leads to a harder decision boundary.

How do you handle imbalanced datasets in SVM?

To handle imbalanced datasets in SVM, you can employ various techniques:

• Adjust the class weights: Assign higher weights to the minority class and lower weights to the majority class. This way, misclassifications in the minority class are penalized more during training.

• Resampling techniques: Oversample the minority class by duplicating or generating synthetic samples, or undersample the majority class by randomly removing samples. This rebalances the dataset.

• Use different evaluation metrics: Instead of accuracy, use evaluation metrics such as precision, recall, F1-score, or area under the precision-recall curve that are more suitable for imbalanced datasets.

How do you handle missing values in SVM?

To handle missing values in SVM, you have a few options:

• Remove samples: If the number of samples with missing values is small, you can remove those samples from the dataset.

• Imputation: If the number of missing values is relatively small within a feature, you can fill them in using imputation techniques such as mean imputation, median imputation, or regression imputation.

• Consider using techniques like support vector data description (SVDD) or one-class SVM, which are designed for anomaly detection and can handle missing values directly.

Explain the process of SVM training.

The process of SVM training involves the following steps:

1. Data preprocessing: Prepare the dataset by performing tasks such as data cleaning, normalization, and feature scaling.

2. Selecting the kernel: Choose an appropriate kernel function based on the data characteristics and the desired decision boundary.

3. Parameter selection: Determine the values of hyperparameters, such as the regularization parameter C and kernel-specific parameters, either through manual tuning or using techniques like cross-validation.

4. Training: Optimize the SVM model by solving the quadratic programming problem using algorithms such as sequential minimal optimization (SMO) or interior point methods.

5. Model evaluation: Assess the performance of the trained SVM model using evaluation metrics such as accuracy, precision, recall, F1-score, or area under the ROC curve.

What are support vectors in SVM?

Support vectors in SVM are the data points from the training dataset that lie closest to the decision hyperplane or violate the margin. These data points are critical in defining the decision boundary and determining the optimal hyperplane. They are the only points that influence the construction of the hyperplane, and the rest of the training data points are irrelevant once the model is trained.

How do you handle categorical variables in SVM?

SVM typically works with numerical feature vectors, so categorical variables need to be converted into a suitable numerical representation. One common approach is one-hot encoding, where each category is transformed into a binary feature. Another approach is ordinal encoding, where categories are assigned ordinal values. Alternatively, you can use kernel functions that can directly handle categorical variables, such as the categorical kernel.

What is the difference between hard margin and soft margin in SVM?

In SVM, hard margin refers to the approach where the decision boundary is required to perfectly separate the classes without any misclassifications. Hard margin SVM assumes that the data is linearly separable. If the data is not linearly separable, the hard margin approach would fail.

Soft margin, on the other hand, allows for misclassifications and violations of the margin. Soft margin SVM handles datasets that are not linearly separable by allowing some data points to be misclassified or fall within the margin. The objective is to find a balance between maximizing the margin and minimizing the number of misclassifications. The C parameter controls the trade-off between margin size and misclassification penalty, with a smaller C value allowing more misclassifications (softer margin) and a larger C value enforcing a stricter margin (harder margin).

How do you choose the optimal hyperparameters in SVM?

To choose the optimal hyperparameters in SVM, you can use techniques like grid search or random search. In grid search, you define a grid of possible values for the hyperparameters and evaluate the performance of the SVM model for each combination using cross-validation. The combination that results in the best performance metric is selected as the optimal set of hyperparameters. Random search randomly samples hyperparameter values from predefined ranges and evaluates the model performance for each set of hyperparameters. This process is repeated for a specified number of iterations, and the best-performing set of hyperparameters is chosen.

Can SVM be used for multi-class classification? If yes, how?

Yes, SVM can be used for multi-class classification. There are two main approaches to handle multi-class classification with SVM:

1. One-vs-One (OvO): Train a separate SVM classifier for each pair of classes. For N classes, N*(N-1)/2 classifiers are trained. During prediction, each classifier assigns a class label, and the class label with the maximum votes across all classifiers is selected as the final prediction.

2. One-vs-All (OvA): Train a single SVM classifier for each class, considering it as the positive class and the rest of the classes as the negative class. During prediction, each classifier assigns a confidence score, and the class with the highest confidence score is selected as the final prediction.

What are the possible applications of SVM?

SVM has a wide range of applications, including:

• Text categorization and sentiment analysis

• Image classification and object recognition

• Handwriting recognition

• Fraud detection

• Bioinformatics, such as protein classification and gene expression analysis

• Face detection and recognition

• Anomaly detection

• Medical diagnosis

• Financial market analysis

• Natural language processing

How does SVM handle outliers in the dataset?

SVM can be robust to outliers due to its dependence on support vectors. Outliers, which are data points located far from the decision boundary, might become support vectors and influence the position of the decision boundary. However, if the outliers are irrelevant or noisy, they can significantly affect the SVM model's performance.

To handle outliers, you can consider the following approaches:

• Outlier removal: Identify and remove outliers from the dataset before training the SVM model.

• Adjusting C parameter: Increase the C value to penalize misclassifications and violations of the margin more heavily, making the SVM model less sensitive to outliers.

• Use robust variants of SVM: There are variants of SVM, such as the Support Vector Data Description (SVDD), that are specifically designed to handle outliers and anomalies by modeling the normal class as a compact region.

Remember, the specific approach to handle outliers depends on the characteristics of your dataset and the specific problem you are trying to solve.

Python Application

Using Sklearn

xxxxxxxxxx
26
1
from sklearn import datasets
2
from sklearn.model_selection import train_test_split
3
from sklearn.svm import SVC
4
from sklearn.metrics import accuracy_score
5

6
# Load the IRIS dataset
7
iris = datasets.load_iris()
8
X = iris.data
9
y = iris.target
10

11
# Split the dataset into training and testing sets
12
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
13

14
# Create an SVM classifier
15
svm_classifier = SVC(kernel='rbf')
16

17
# Train the classifier
18
svm_classifier.fit(X_train, y_train)
19

20
# Make predictions on the test set
21
y_pred = svm_classifier.predict(X_test)
22

23
# Evaluate the accuracy of the classifier
24
accuracy = accuracy_score(y_test, y_pred)
25
print("Accuracy:", accuracy)

In this example, we first load the IRIS dataset using the datasets.load_iris() function from scikit-learn. We then split the dataset into training and testing sets using train_test_split() function. Next, we create an SVM classifier using SVC class from the svm module. In this case, we use the radial basis function (RBF) kernel by setting kernel='rbf'.

We train the SVM classifier on the training data using the fit() method. Then, we use the trained classifier to make predictions on the test set with the predict() method. Finally, we evaluate the accuracy of the classifier by comparing the predicted labels with the actual labels from the test set using the accuracy_score() function.

Note: The example assumes that you have scikit-learn (sklearn) library installed. If you don't, you can install it using pip install scikit-learn.

From Scratch

The main goal of SVM

We looked at the working of SVM in detail in previous articles, but to give a quick understanding of the goal of SVM let's explain it! The main goal of SVM is the maximization of margins between two different classes. That means that you want to make sure that as many points in one class are on one side of the decision boundary and as many points in the other class are on the other side.

When this happens, all points with a higher degree of separation will be correctly classified while all points with a lower degree of separation will be misclassified.

So when the marginal distance between these two classes is at their maximum, they become the optimal solution for maximizing margin and minimizing risk. As such, it becomes a lot easier to classify new points without any error because they can just be placed on either side of the decision boundary based on which class it belongs to. If there are errors though then there's always something called regularization which allows us to penalize models so that they generalize better for new data points.

The equation for Soft Margin SVM

The regularization term for SVM will look like this:

This term is known as the regularizer which we need to use for maximizing the margin and minimizing the loss.

When adding two terminologies for our gradient descent to work, ie, the number of errors in training(C), and the sum of the value of error($\sum _{i=1}^n{ϵ}_i$$\sum_{i=1}^{n}\epsilon_i$) the equation can be written as:

This particular error term added allows some classification errors to occur for avoiding overfitting of our model, ie, the hyperplane will not be changed if there are small errors in classification. This model is known as a Soft Margin SVM.

Now let's rewrite this equation in the form of a Loss function view. The Loss function we are using here is known as the Hinge Loss function which would look like this:

Let's rewrite the optimization term, including the Hinge Loss function:

This is the term we need to optimize using our gradient descent algorithm in order to obtain parameters w(weights) and b(bias)

Implementing SVM from scratch in python

Writing the SVM class

13
1
# svm.py
2

3

4
import numpy as np
5

6

7
class SVM:
8

9
    def __init__(self, C = 1.0):
10
        # C = error term
11
        self.C = C
12
        self.w = 0
13
        self.b = 0

First, we created a class SVM and initialized some values. The C term is known as the error term which we need to add for optimizing the function

Hinge Loss calculation

x
1
# Hinge Loss Function / Calculation
2
def hingeloss(self, w, b, x, y):
3
    # Regularizer term
4
    reg = 0.5 * (w * w)
5

6
    for i in range(x.shape[0]):
7
        # Optimization term
8
        opt_term = y[i] * ((np.dot(w, x[i])) + b)
9

10
        # calculating loss
11
        loss = reg + self.C * max(0, 1-opt_term)
12
    return loss[0][0]

Let's understand what's happening here. First, we are calculating the value of the regularizer term and assign it to variable reg. Then iterating over the number of samples and calculating the loss using the optimization function.

Gradient Descent optimization

Now let's create the gradient descent function inside the fit method in order to get the best parameters w and b.

57
1
def fit(self, X, Y, batch_size=100, learning_rate=0.001, epochs=1000):
2
    # The number of features in X
3
    number_of_features = X.shape[1]
4

5
    # The number of Samples in X
6
    number_of_samples = X.shape[0]
7

8
    c = self.C
9

10
    # Creating ids from 0 to number_of_samples - 1
11
    ids = np.arange(number_of_samples)
12

13
    # Shuffling the samples randomly
14
    np.random.shuffle(ids)
15

16
    # creating an array of zeros
17
    w = np.zeros((1, number_of_features))
18
    b = 0
19
    losses = []
20

21
    # Gradient Descent logic
22
    for i in range(epochs):
23
        # Calculating the Hinge Loss
24
        l = self.hingeloss(w, b, X, Y)
25

26
        # Appending all losses 
27
        losses.append(l)
28

29
        # Starting from 0 to the number of samples with batch_size as interval
30
        for batch_initial in range(0, number_of_samples, batch_size):
31
            gradw = 0
32
            gradb = 0
33

34
            for j in range(batch_initial, batch_initial + batch_size):
35
                if j < number_of_samples:
36
                    x = ids[j]
37
                    ti = Y[x] * (np.dot(w, X[x].T) + b)
38

39
                    if ti > 1:
40
                        gradw += 0
41
                        gradb += 0
42
                    else:
43
                        # Calculating the gradients
44

45
                        #w.r.t w 
46
                        gradw += c * Y[x] * X[x]
47
                        # w.r.t b
48
                        gradb += c * Y[x]
49

50
            # Updating weights and bias
51
            w = w - learning_rate * w + learning_rate * gradw
52
            b = b + learning_rate * gradb
53

54
    self.w = w
55
    self.b = b
56

57
    return self.w, self.b, losses  

What happens in this fit method is really simple, we are trying to reduce the loss in consecutive iterations and find the best parameters w and b. Note that here we are using Batch Gradient Descent. The weights(w) and bias(b) are updated in every iteration using the gradients and the learning rate resulting in the minimization of the loss. When the optimal parameters are found the method simply returns it along with the losses.

Predict Method

4
1
def predict(self, X):
2

3
    prediction = np.dot(X, self.w[0]) + self.b # w.x + b
4
    return np.sign(prediction)

Performing Classification

Alright, we have created an SVM class only with the help of NumPy. Now let's do some classification to see our model in action.

Creating random dataset

22
1
# prediction.py
2

3

4
from sklearn import datasets
5
import matplotlib.pyplot as plt
6
import numpy as np
7
from sklearn.metrics import accuracy_score
8
from sklearn.model_selection import train_test_split
9
from svm import SVM
10

11
# Creating dataset
12
X, y = datasets.make_blobs(
13

14
        n_samples = 100, # Number of samples
15
        n_features = 2, # Features
16
        centers = 2,
17
        cluster_std = 1,
18
        random_state=40
19
    )
20

21
# Classes 1 and -1
22
y = np.where(y == 0, -1, 1)

Splitting the dataset

xxxxxxxxxx
1
1
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.5, random_state=42)

Training the SVM model

3
1
svm = SVM()
2

3
w, b, losses = svm.fit(X_train, y_train)

Making predictions and testing accuracy

xxxxxxxxxx
1
prediction = svm.predict(X_test)
2

3
# Loss value
4
lss = losses.pop()
5

6
print("Loss:", lss)
7
print("Prediction:", prediction)
8
print("Accuracy:", accuracy_score(prediction, y_test))
9
print("w, b:", [w, b])
10

11

12
----
13

14

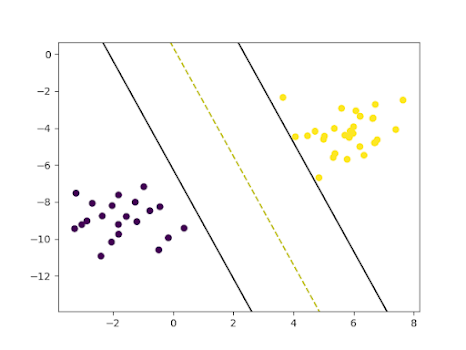
15
Loss: 0.0991126738798482
16
Prediction: [-1.  1. -1. -1.  1.  1.  1.  1. -1.  1. -1. -1.  1.  1. -1. -1.  1. -1.
17
  1. -1.  1.  1. -1.  1.  1.  1. -1. -1. -1. -1.  1. -1. -1.  1.  1. -1.
18
  1. -1. -1.  1.  1.  1.  1.  1.  1. -1.  1.  1.  1.  1.]
19
Accuracy: 1.0
20
w, b: [array([[0.44477983, 0.15109913]]), 0.05700000000000004]

Visualizing SVM

Visualizing SVM is one of the best ways to find how it is being fitted to the training data. We can do this using the matplotlib package.

40
1
# Visualizing the scatter plot of the dataset
2
def visualize_dataset():
3
    plt.scatter(X[:, 0], X[:, 1], c=y)
4

5

6
# Visualizing SVM
7
def visualize_svm():
8

9
    def get_hyperplane_value(x, w, b, offset):
10
        return (-w[0][0] * x + b + offset) / w[0][1]
11

12
    fig = plt.figure()
13
    ax = fig.add_subplot(1,1,1)
14
    plt.scatter(X_test[:, 0], X_test[:, 1], marker="o", c=y_test)
15

16
    x0_1 = np.amin(X_test[:, 0])
17
    x0_2 = np.amax(X_test[:, 0])
18

19
    x1_1 = get_hyperplane_value(x0_1, w, b, 0)
20
    x1_2 = get_hyperplane_value(x0_2, w, b, 0)
21

22
    x1_1_m = get_hyperplane_value(x0_1, w, b, -1)
23
    x1_2_m = get_hyperplane_value(x0_2, w, b, -1)
24

25
    x1_1_p = get_hyperplane_value(x0_1, w, b, 1)
26
    x1_2_p = get_hyperplane_value(x0_2, w, b, 1)
27

28
    ax.plot([x0_1, x0_2], [x1_1, x1_2], "y--")
29
    ax.plot([x0_1, x0_2], [x1_1_m, x1_2_m], "k")
30
    ax.plot([x0_1, x0_2], [x1_1_p, x1_2_p], "k")
31

32
    x1_min = np.amin(X[:, 1])
33
    x1_max = np.amax(X[:, 1])
34
    ax.set_ylim([x1_min - 3, x1_max + 3])
35

36
    plt.show()
37

38

39
visualize_dataset()
40
visualize_svm()

Visualization of dataset

Visualization of SVM on the test set

Complete version of SVM algorithm

87
1
import numpy as np
2

3

4
class SVM:
5

6
    def __init__(self, C = 1.0):
7
        # C = error term
8
        self.C = C
9
        self.w = 0
10
        self.b = 0
11

12
    # Hinge Loss Function / Calculation
13
    def hingeloss(self, w, b, x, y):
14
        # Regularizer term
15
        reg = 0.5 * (w * w)
16

17
        for i in range(x.shape[0]):
18
            # Optimization term
19
            opt_term = y[i] * ((np.dot(w, x[i])) + b)
20

21
            # calculating loss
22
            loss = reg + self.C * max(0, 1-opt_term)
23
        return loss[0][0]
24

25
    def fit(self, X, Y, batch_size=100, learning_rate=0.001, epochs=1000):
26
        # The number of features in X
27
        number_of_features = X.shape[1]
28

29
        # The number of Samples in X
30
        number_of_samples = X.shape[0]
31

32
        c = self.C
33

34
        # Creating ids from 0 to number_of_samples - 1
35
        ids = np.arange(number_of_samples)
36

37
        # Shuffling the samples randomly
38
        np.random.shuffle(ids)
39

40
        # creating an array of zeros
41
        w = np.zeros((1, number_of_features))
42
        b = 0
43
        losses = []
44

45
        # Gradient Descent logic
46
        for i in range(epochs):
47
            # Calculating the Hinge Loss
48
            l = self.hingeloss(w, b, X, Y)
49

50
            # Appending all losses 
51
            losses.append(l)
52
            
53
            # Starting from 0 to the number of samples with batch_size as interval
54
            for batch_initial in range(0, number_of_samples, batch_size):
55
                gradw = 0
56
                gradb = 0
57

58
                for j in range(batch_initial, batch_initial+ batch_size):
59
                    if j < number_of_samples:
60
                        x = ids[j]
61
                        ti = Y[x] * (np.dot(w, X[x].T) + b)
62

63
                        if ti > 1:
64
                            gradw += 0
65
                            gradb += 0
66
                        else:
67
                            # Calculating the gradients
68

69
                            #w.r.t w 
70
                            gradw += c * Y[x] * X[x]
71
                            # w.r.t b
72
                            gradb += c * Y[x]
73

74
                # Updating weights and bias
75
                w = w - learning_rate * w + learning_rate * gradw
76
                b = b + learning_rate * gradb
77
        
78
        self.w = w
79
        self.b = b
80

81
        return self.w, self.b, losses
82

83
    def predict(self, X):
84
        
85
        prediction = np.dot(X, self.w[0]) + self.b # w.x + b
86
        return np.sign(prediction)
87