梯度下降（Gradient Descent）

Summary

梯度下降是一种通过计算函数梯度并沿着梯度反方向更新参数的优化算法，用于寻找函数的最小值，常用于机器学习和数学优化问题中。

Gradient descent is an optimization algorithm that iteratively updates parameters by computing and moving in the direction of the function's gradient, aiming to find the minimum of the function.

Key Takeaways

1. 梯度下降是一种迭代优化算法，用于通过调整参数来找到函数的最小值。

2. 它依赖于计算每次迭代中函数的梯度（导数），以确定最陡下降的方向。

3. 学习率决定了每次迭代中的步长大小，影响算法的收敛速度和稳定性。

4. 梯度下降通过在梯度的反方向更新参数，逐渐接近最小值。

5. 它可用于凸函数和非凸函数，尽管收敛保证在两种情况下略有不同。

6. 成本函数或损失函数的选择至关重要，因为它决定了在机器学习模型中所优化的目标。

7. 梯度下降有不同的变体，包括批量梯度下降、随机梯度下降和小批量梯度下降，每种变体都有其优点和缺点。

8. 梯度下降可能会陷入局部最小值，但动量、自适应学习率和正则化等技术可以帮助减轻这个问题。

9. 收敛准则通常使用梯度范数很小或达到最大迭代次数等条件来停止算法。

10. 梯度下降在机器学习、深度学习和神经网络训练中被广泛应用，使模型能够从数据中学习并优化性能。

1. Gradient descent is an iterative optimization algorithm used to find the minimum of a function by adjusting its parameters.

2. It relies on computing the gradient (derivative) of the function at each iteration to determine the direction of steepest descent.

3. The learning rate determines the step size taken in each iteration, influencing the convergence speed and stability of the algorithm.

4. Gradient descent operates by updating the parameters in the opposite direction of the gradient, gradually approaching the minimum.

5. It can be used for both convex and non-convex functions, although convergence guarantees differ between the two cases.

6. The choice of the cost function or loss function is crucial, as it determines the objective being optimized in machine learning models.

7. There are different variations of gradient descent, including batch gradient descent, stochastic gradient descent, and mini-batch gradient descent, each with its own advantages and drawbacks.

8. Gradient descent may get trapped in local minima, but techniques like momentum, adaptive learning rates, and regularization can help mitigate this issue.

9. Convergence criteria, such as a small gradient norm or reaching a maximum number of iterations, are typically used to stop the algorithm.

10. Gradient descent is widely used in machine learning, deep learning, and neural network training, enabling models to learn from data and optimize their performance.

Interview Questions

什么是梯度下降？它在机器学习中的作用是什么？

梯度下降基本概念

梯度下降是一种优化算法，用于在机器学习中寻找函数的最小值。它通过计算函数的梯度（导数）来确定最陡下降的方向，并在每次迭代中更新参数，逐步接近最优解。

为什么用梯度下降？

梯度下降在机器学习中的作用是通过最小化损失函数来优化模型的参数，使模型能够更准确地进行预测和分类。

1. 模型训练：在机器学习中，我们需要通过训练数据来调整模型的参数，以使其能够对未见过的数据进行准确的预测。梯度下降通过优化参数，使模型能够逐渐改善其预测能力，最大限度地减少预测误差。

2. 参数优化：梯度下降通过计算损失函数关于参数的梯度，确定参数更新的方向和步长。通过反复迭代更新参数，梯度下降能够逐步接近损失函数的最小值，找到最优的参数配置，使模型能够达到最佳的性能。

3. 深度学习中的神经网络训练：在深度学习中，神经网络模型具有大量的参数，需要通过梯度下降来训练这些参数。梯度下降通过反向传播算法计算每个参数的梯度，并根据梯度的反方向更新参数，以优化网络的性能。梯度下降在神经网络的训练中扮演着关键的角色，使网络能够逐层地学习特征表示，从而提高预测的准确性。

梯度下降的主要步骤是什么？请解释每个步骤的含义。

1. 初始化参数：选择初始参数的值。

2. 计算梯度：计算函数在当前参数值处的梯度（导数）。梯度表示函数在给定点的变化率和方向。

3. 更新参数：根据学习率确定的步长，沿着梯度的反方向更新参数值。学习率决定了每次迭代中参数更新的大小。

4. 重复迭代：重复执行步骤2和步骤3，直到满足停止条件，如达到最大迭代次数或梯度变化很小。

学习率的选择对梯度下降的性能有何影响？如何选择适当的学习率？

学习率的选择对梯度下降的性能具有重要影响。学习率太小会导致收敛速度慢，需要更多的迭代次数才能达到最优解；学习率太大可能会导致震荡或无法收敛。

适当的学习率应根据具体问题进行调整，常见的选择方法包括：

• 网格搜索：尝试不同的学习率值，并根据验证集或交叉验证的性能选择最佳学习率。

• 学习率衰减：开始时使用较大的学习率，随着迭代的进行逐渐减小学习率，使其更接近最优解。

• 自适应学习率：一些优化算法（如Adam、Adagrad、RMSprop）会根据梯度的统计信息自动调整学习率，以提高性能和收敛速度。

适当的学习率选择可以加快算法的收敛速度并提高优化结果的质量。然而，过大或过小的学习率都可能导致性能下降，因此需要进行适当的调整和实验来找到最佳的学习率。

学习率过大或过小都会对梯度下降算法的性能产生负面影响，具体表现如下：

1. 学习率过大：

   • 收敛困难或不稳定：如果学习率过大，每次参数更新的步长会很大，可能会导致梯度下降算法无法收敛或在最小值附近震荡，无法稳定地找到最优解。

   • 跳过最优解：学习率过大可能会导致参数跳过最优解点，错过损失函数的最小值，从而导致模型性能下降。

2. 学习率过小：

   • 收敛缓慢：如果学习率过小，每次参数更新的步长会很小，可能需要更多的迭代次数才能达到最优解，导致收敛速度缓慢。

   • 陷入局部最小值：学习率过小可能会使梯度下降算法陷入局部最小值，无法跳出该局部最小值并继续搜索更优的解。

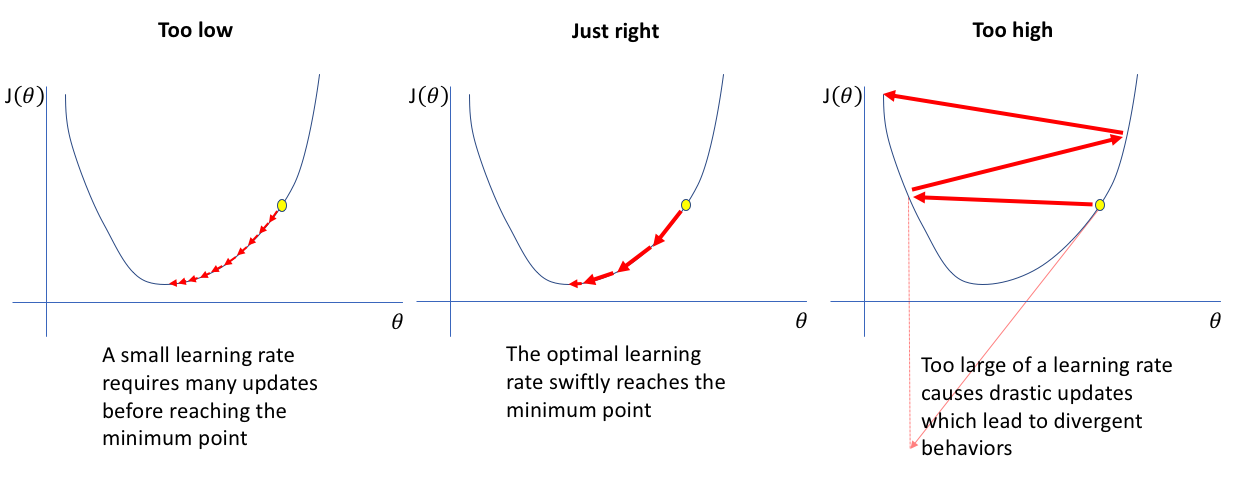
选择合适的学习率很重要。合适的学习率应该能够在合理的迭代次数内收敛到最优解，同时避免收敛困难、震荡或陷入局部最小值。通常需要通过实验和调整来选择最佳的学习率。一些自适应学习率算法（如Adam、Adagrad、RMSprop）可以根据梯度的统计信息自动调整学习率，从而更好地平衡收敛速度和性能。

梯度下降有哪些常见的变体？它们之间有什么区别？

1. 批量梯度下降（Batch Gradient Descent）：在每次迭代中，使用整个训练数据集计算损失函数的梯度，然后更新参数。它需要存储整个数据集，计算量较大，但通常具有较好的收敛性。

   • 梯度计算：在每次迭代中，批量梯度下降使用整个训练数据集计算损失函数关于参数的梯度。这意味着它需要遍历整个数据集并计算每个样本对梯度的贡献。

   • 参数更新：在梯度计算完成后，批量梯度下降通过将参数沿着梯度的相反方向进行更新来最小化损失函数。更新的步长由学习率控制。

   • 每次迭代使用全部数据：批量梯度下降在每次迭代中都使用整个训练数据集，因此它的参数更新是基于全部数据的梯度信息。

   • 收敛性：由于使用整个数据集计算梯度，批量梯度下降通常具有较好的收敛性。它可以更准确地估计梯度，因此在一定迭代次数后能够收敛到较好的解。

   • 计算复杂度：相对于随机梯度下降和小批量梯度下降，批量梯度下降的计算复杂度较高。因为它需要计算整个数据集的梯度，对于大规模数据集或高维数据而言，计算量较大。

   • 内存要求：批量梯度下降需要存储整个数据集，因此对内存的要求较高。对于较大的数据集，可能需要额外的内存管理策略，如分批加载数据或使用分布式计算。

2. 随机梯度下降（Stochastic Gradient Descent）：在每次迭代中，随机选择一个样本来计算损失函数的梯度，并更新参数。它具有较低的计算复杂度，但可能导致参数更新的方向不稳定，存在一定的随机性。

   • 梯度计算：在每次迭代中，随机梯度下降使用单个样本或随机选择的小批量样本来计算损失函数关于参数的梯度。与批量梯度下降不同，它不需要遍历整个数据集。

   • 参数更新：在梯度计算完成后，随机梯度下降通过将参数沿着梯度的相反方向进行更新来最小化损失函数。更新的步长由学习率控制。

   • 随机性：由于每次迭代使用的是单个样本或小批量样本，随机梯度下降的参数更新具有一定的随机性。这也导致了它的更新方向可能不太稳定，但有助于避免陷入局部最优解。

   • 迭代次数：由于使用随机样本进行梯度计算和参数更新，随机梯度下降通常需要较少的迭代次数才能达到收敛。每个迭代的计算开销较小，使其在大规模数据集上更高效。

   • 内存要求：随机梯度下降只需要存储当前样本或小批量样本的信息，对内存要求较低。因此，它适用于大规模数据集或具有高维特征的问题。

   • 收敛性：由于使用随机样本进行梯度估计，随机梯度下降的收敛性可能不如批量梯度下降稳定。在一定程度上，随机梯度下降可能陷入局部最小值，但也有机会跳出局部最小值并找到更好的解。

3. 小批量梯度下降（Mini-Batch Gradient Descent）：在每次迭代中，随机选择一小批样本（通常为2到几百个）来计算损失函数的梯度，并更新参数。小批量梯度下降综合了批量梯度下降和随机梯度下降的优点，可以在一定程度上平衡收敛速度和参数更新的稳定性。

   • 梯度计算：在每次迭代中，小批量梯度下降使用一小批样本（通常为2到几百个）来计算损失函数关于参数的梯度。这一小批样本的大小是可以调整的。

   • 参数更新：在梯度计算完成后，小批量梯度下降通过将参数沿着梯度的相反方向进行更新来最小化损失函数。更新的步长由学习率控制。

   • 每次迭代使用部分数据：小批量梯度下降在每次迭代中使用一小批样本来计算梯度，而不是整个数据集。这样可以在一定程度上平衡批量梯度下降和随机梯度下降的优势。

   • 计算复杂度：相对于批量梯度下降，小批量梯度下降的计算复杂度较低。它不需要计算整个数据集的梯度，而是仅计算一小批样本的梯度，因此在大规模数据集上具有较好的可扩展性。

   • 内存要求：小批量梯度下降需要存储一小批样本的信息，内存要求介于批量梯度下降和随机梯度下降之间。对于较大的数据集，仍然需要适当的内存管理策略。

   • 收敛性：小批量梯度下降相对于随机梯度下降具有较好的收敛性。它的梯度估计比随机梯度下降更稳定，同时相对于批量梯度下降，更新的频率更高，有助于更快地收敛。

这些变体之间的主要区别在于参数更新的频率和计算复杂度。批量梯度下降需要计算整个数据集的梯度，适用于较小的数据集，但计算量较大。随机梯度下降每次只计算一个样本的梯度，计算量较小，但参数更新可能不稳定。小批量梯度下降在每次迭代中计算一小批样本的梯度，可以在一定程度上平衡计算效率和参数更新的稳定性。

如何解决梯度下降中的局部最小值问题？

解决梯度下降中的局部最小值问题是一个挑战，因为梯度下降算法可能会陷入局部最小值而无法找到全局最小值。以下是几种常用的方法来解决这个问题：

1. 初始化策略：通过合适的参数初始化可以增加逃离局部最小值的机会。可以尝试使用不同的初始参数值进行多次运行，并选择具有较低损失的结果作为最终模型。

2. 学习率调整：学习率是梯度下降算法中的重要参数，对于避免陷入局部最小值至关重要。过大的学习率可能导致参数在梯度下降过程中发散，而过小的学习率可能使算法收敛速度过慢。可以尝试使用学习率调度策略，如学习率衰减或自适应学习率方法（如Adam、Adagrad等），以动态调整学习率的大小。

3. 随机性引入：在梯度下降算法中引入一定程度的随机性可以帮助避免陷入局部最小值。例如，使用随机梯度下降或小批量梯度下降来计算梯度，而不是批量梯度下降，可以在每次迭代中引入随机性。

4. 正则化方法：正则化方法可以帮助克服局部最小值问题。例如，L1正则化（Lasso）和L2正则化（Ridge）可以引入参数稀疏性，防止参数陷入某些局部最小值。

5. 梯度初始化：对于某些模型，合适的梯度初始化方法可以帮助模型避免陷入局部最小值。例如，在深度神经网络中，使用一些高效的初始化方法，如Xavier初始化或He初始化，可以提高模型的训练效果。

6. 模型复杂性：增加模型的复杂性（如增加层数、增加参数量）可以提高模型的拟合能力，从而减少陷入局部最小值的可能性。然而，增加模型复杂性也会增加过拟合的风险，需要进行适当的正则化和模型选择。

梯度下降的收敛条件是什么？如何确定算法是否已经收敛？

梯度下降的收敛条件通常是通过判断算法是否达到了预定的停止条件。常见的收敛条件有以下几种：

1. 梯度阈值：当梯度的范数（向量的长度）小于某个设定的阈值时，可以认为算法已经收敛。

2. 目标函数值变化：当目标函数值的变化小于某个设定的阈值时，可以认为算法已经收敛。通常需要比较连续几次迭代中的目标函数值，如果变化足够小，则判定为收敛。

3. 参数变化：当参数的变化小于某个设定的阈值时，可以认为算法已经收敛。与目标函数值类似，需要比较连续几次迭代中的参数变化。

4. 迭代次数：设定一个最大迭代次数，当达到该次数时，算法停止迭代。

确定算法是否已经收敛可以根据以下策略：

1. 观察目标函数值的变化：监控目标函数值在每次迭代中的变化情况，如果变化足够小并且在一段时间内保持稳定，则可以认为算法已经收敛。

2. 观察参数的变化：监控参数在每次迭代中的变化情况，如果变化足够小并且在一段时间内保持稳定，则可以认为算法已经收敛。

3. 判断梯度的范数：计算梯度的范数，并与预设的阈值进行比较，如果梯度的范数小于阈值，则可以认为算法已经收敛。

4. 设定最大迭代次数：如果达到了预设的最大迭代次数，可以判定算法停止迭代，即达到了收敛条件。

在实际应用中，根据具体问题和算法的特点选择适合的收敛条件，一般会结合多个条件进行判断。同时，观察目标函数值的变化曲线、参数的变化曲线以及梯度的变化曲线也是一种直观判断算法是否收敛的方式。

在梯度下降中，什么是动量（momentum）？它如何改善算法的性能？

在梯度下降中，动量（momentum）是一种用于加速收敛和减少梯度下降算法震荡的技术。

动量可以理解为模拟物理力学中的动量概念，它在更新参数时考虑了过去梯度的累积影响。具体来说，动量算法引入了一个动量项，它表示过去梯度更新的加权平均。在每次参数更新时，动量项会根据当前梯度的方向和大小进行调整。

动量的更新公式如下：

v = β * v - α * ∇J(θ) θ = θ + v

其中，v是动量项，β是动量系数（通常取值范围为0到1之间），α是学习率，∇J(θ)是当前参数位置的梯度。

动量的作用是在参数更新时考虑之前的梯度趋势。如果当前梯度和过去梯度的方向一致，那么动量项会增强梯度下降的力度；如果当前梯度和过去梯度的方向相反，那么动量项会减缓梯度下降的力度。这样可以在参数空间中更快地穿过平坦区域，避免陷入局部最小值，并且减少震荡，提高算法的稳定性。

动量的引入能够加速梯度下降的收敛速度，特别是在面对高度曲折的损失函数表面时。它还有助于跳出局部极小点，并且在参数更新方向不断变化时，能够提供一定的稳定性。动量算法常用于深度神经网络训练中，能够加速收敛、减少震荡，并且有助于避免陷入鞍点等问题。

当目标函数具有多个参数时，如何同时更新它们？

梯度下降在神经网络训练中的应用是怎样的？有没有其他优化算法可以替代梯度下降？

当目标函数具有多个参数时，可以使用梯度下降算法同时更新它们。梯度下降算法中的参数更新规则是对每个参数进行更新，使其朝着梯度的反方向移动，从而最小化目标函数。

具体而言，对于每个参数 θ_i，其更新规则为：

${\theta }_i={\theta }_i-\alpha \ast \frac{\partial J}{\partial {\theta }_i}$$θ_i = θ_i - α * \frac{\partial J}{\partial θ_i}$

其中，α 是学习率，$\frac{\partial J}{\partial {\theta }_i}$$\frac{∂J}{∂θ_i}$ 是目标函数关于参数 θi 的偏导数，也称为参数 θi 的梯度。

在实践中，可以将所有参数的更新步骤组合在一起，同时更新它们。具体步骤如下：

1. 计算目标函数关于每个参数的梯度：$\frac{\partial J}{\partial {\theta }_1},\frac{\partial J}{\partial {\theta }_2},...,\frac{\partial J}{\partial {\theta }_n}$$\frac{∂J}{∂θ_1}, \frac{∂J}{∂θ_2}, ..., \frac{∂J}{∂θ_n}$。

2. 对于每个参数 ${\theta }_i$$θ_i$，应用参数更新规则：${\theta }_i={\theta }_i-\alpha \ast \frac{\partial J}{\partial {\theta }_i}$$θ_i = θ_i - α * \frac{∂J}{∂θ_i}$。

通过同时更新所有参数，梯度下降算法能够在参数空间中搜索更优的解，最小化目标函数。这样可以有效地优化多参数的模型，并找到使目标函数最小化的最佳参数组合。