朴素贝叶斯
判别模型与生成模型
判别模型 我们知道,其实机器学习就是想办法从特征 X X X y y y p ( y ∣ X ) p(y|X) p ( y ∣ X )
那么对于判别模型,我们只考虑去估计条件概率,是在有限样本的条件下建立判别函数,不考虑样本的产生模型,直接研究预测模型,也可以理解为在二分类问题中,p ( y = 1 ∣ X ) + p ( y = 0 ∣ X ) = 1 p(y=1|X) + p(y=0|X) = 1 p ( y = 1 ∣ X ) + p ( y = 0 ∣ X ) = 1 1 1 1
生成模型 而生成式模型求得 p ( y , X ) p(y,X) p ( y , X ) X X X
什么是朴素贝叶斯?
首先,朴素贝叶斯是个生成模型,朴素贝叶斯分类器是一系列以假设特征之间强独立 下运用贝叶斯定理 为基础的简单地概率分类器。
朴素贝叶斯自20世纪50年代已广泛研究。在20世纪60年代初就以另外一个名称引入到文本信息检索 界中,[1] :488 并仍然是文本分类 的一种热门(基准)方法,文本分类是以词频 为特征判断文件所属类别或其他(如垃圾邮件 、合法性、体育或政治等等)的问题。通过适当的预处理,它可以与这个领域更先进的方法(包括支持向量机 )相竞争。[2] 它在自动医疗诊断 中也有应用。[3]
朴素贝叶斯是一种构建分类器的简单方法。该分类器模型会给问题实例分配用特征 值表示的类标签,类标签取自有限集合。它不是训练这种分类器的单一算法,而是一系列基于相同原理的算法:所有朴素贝叶斯分类器都假定样本每个特征与其他特征都不相关 。举个例子,如果一种水果其具有红,圆,直径大概3英寸等特征,该水果可以被判定为是苹果。尽管这些特征相互依赖 或者有些特征由其他特征决定,然而朴素贝叶斯分类器认为这些属性在判定该水果是否为苹果的概率分布上独立的。
对于某些类型的概率模型,在监督式学习 的样本集中能获取得非常好的分类效果。在许多实际应用中,朴素贝叶斯模型参数估计使用最大似然估计 方法;换而言之,在不用到贝叶斯概率 或者任何贝叶斯模型的情况下,朴素贝叶斯模型也能奏效。
尽管是带着这些朴素思想和过于简单化的假设,但朴素贝叶斯分类器在很多复杂的现实情形中仍能够获取相当好的效果。2004年,一篇分析贝叶斯分类器问题的文章揭示了朴素贝叶斯分类器获取看上去不可思议的分类效果的若干理论上的原因。[5] 尽管如此,2006年有一篇文章详细比较了各种分类方法,发现更新的方法(如决策树 和随机森林 )的性能超过了贝叶斯分类器。[6]
朴素贝叶斯分类器的一个优势在于只需要根据少量的训练数据估计出必要的参数(变量的均值和方差)。由于变量独立假设,只需要估计各个变量的方法,而不需要确定整个协方差矩阵 。
核心思想:贝叶斯公式,独立性假设 第一部分:贝叶斯公式 理论上,概率模型分类器是一个条件概率模型,这个我们已经并不陌生了,也就是要求出:
p ( y ∣ X ) p(y|X) p ( y ∣ X ) y y y X = X 1 , X 2 , ⋯ , X n X = X_1,X_2, \cdots,X_n X = X 1 , X 2 , ⋯ , X n n n n
p ( y ∣ X ) = p ( y ) ( p ( X ∣ y ) p ( X ) p(y|X) = \frac{p(y)(p(X|y)}{p(X)} p ( y ∣ X ) = p ( X ) p ( y ) ( p ( X ∣ y )
用简单的语言可以表示为:
举个例子,假如我们有一副扑克,我们想知道在给定它是一张带人的牌的情况下,我们抽的牌是king的概率。所以根据贝叶斯公式,我们知道
p( King ) 等于 4/52 因为在一副牌里面有 4 张Kingp( Face | King) 等于 1 因为所有的king都是属于带人的牌p( Face ) 等于 12/52 因为每一个花色都有 3 张带人的牌,总共有 12 张
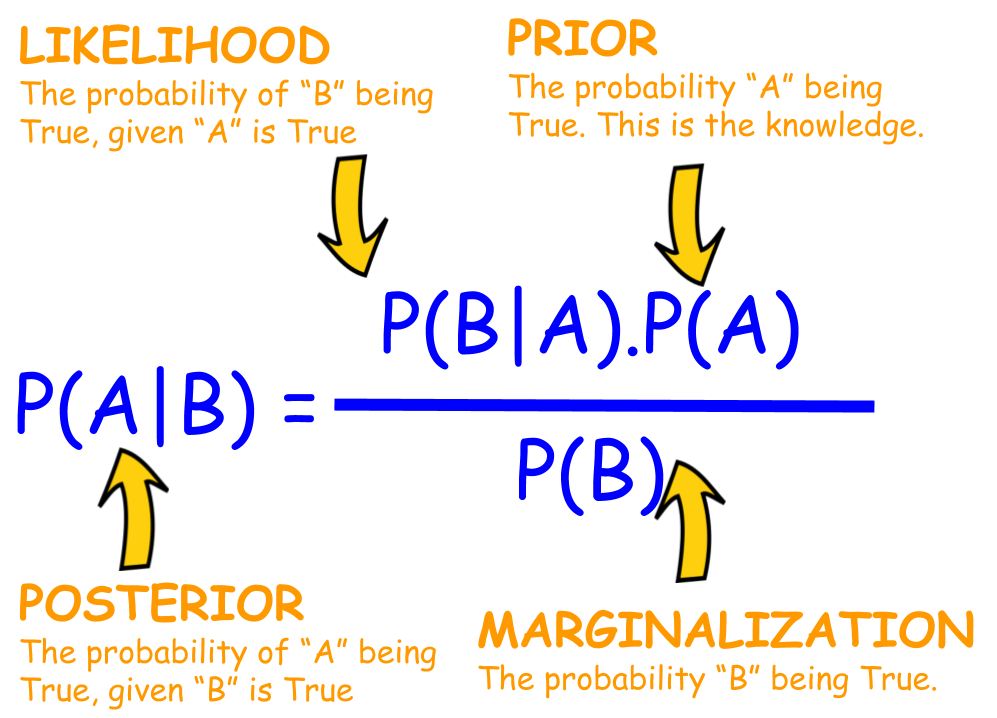
接下来这个式子是我们会经常遇到的
p o s t e r i o r = p r i o r × l i k e l i h o o d e v i d e n c e posterior = \frac{prior \times likelihood}{evidence} p o s t e r i o r = e v i d e n c e p r i o r × l i k e l i h o o d
而实际中,我们只关心分式的分子部分, 因为分母不依赖于 y y y X X X 联合分布 模型。
p ( y , X = X 1 , X 2 , ⋯ , X n ) p(y, X = X_1,X_2, \cdots,X_n) p ( y , X = X 1 , X 2 , ⋯ , X n )
重复使用链式法则,可以将该式写成条件概率的形式,如下:p ( y , X 1 , X 2 , ⋯ , X n ) ∝ p ( y ) p ( X 1 , X 2 , ⋯ , X n ∣ y ) ∝ p ( y ) p ( X 1 ∣ y ) p ( X 2 , ⋯ , X n ∣ y , X 1 ) ∝ p ( y ) p ( X 1 ∣ y ) p ( X 2 ∣ y , X 1 ) p ( X 3 , ⋯ , X n ∣ y , X 1 , X 2 ) ⋯ ∝ p ( y ) p ( X 1 ∣ y ) p ( X 2 ∣ y , X 1 ) p ( X 3 ∣ y , X 1 , X 2 ) ⋯ p ( X n ∣ y , X 1 , X 2 , ⋯ , X n − 1 )
\begin{aligned}
p(y, X_1,X_2, \cdots,X_n) \\
&\propto p(y)p(X_1,X_2, \cdots,X_n|y) \\
&\propto p(y)p(X_1|y)p(X_2,\cdots,X_n|y,X_1) \\
&\propto p(y)p(X_1|y)p(X_2|y,X_1)p(X_3,\cdots,X_n|y,X_1,X_2) \\
&\cdots \\
&\propto p(y)p(X_1|y)p(X_2|y,X_1)p(X_3|y,X_1,X_2)\cdots p(X_n|y,X_1,X_2,\cdots,X_{n-1})
\end{aligned}
p ( y , X 1 , X 2 , ⋯ , X n ) ∝ p ( y ) p ( X 1 , X 2 , ⋯ , X n ∣ y ) ∝ p ( y ) p ( X 1 ∣ y ) p ( X 2 , ⋯ , X n ∣ y , X 1 ) ∝ p ( y ) p ( X 1 ∣ y ) p ( X 2 ∣ y , X 1 ) p ( X 3 , ⋯ , X n ∣ y , X 1 , X 2 ) ⋯ ∝ p ( y ) p ( X 1 ∣ y ) p ( X 2 ∣ y , X 1 ) p ( X 3 ∣ y , X 1 , X 2 ) ⋯ p ( X n ∣ y , X 1 , X 2 , ⋯ , X n − 1 )
第二部分:条件独立假设 从现在开始, “朴素”的条件独立假设开始发挥作用,什么叫条件独立 呢?当两个事件 A A A B B B Y Y Y A A A B B B A A A B B B Y Y Y A A A B B B B B B A A A
所以我们假设每个特征 X i X_i X i X j X_j X j j ≠ i j \neq i j = i
p ( X i ∣ y , X j ) = p ( X i ∣ y ) p(X_i|y,X_j) = p(X_i|y) p ( X i ∣ y , X j ) = p ( X i ∣ y )
对于 i ≠ j i \neq j i = j
p ( y ∣ X 1 , X 2 , ⋯ , X n ) ∝ p ( y , X 1 , X 2 , ⋯ , X n ) ∝ p ( y ) p ( X 1 ∣ y ) p ( X 2 ∣ y ) p ( X 3 ∣ y ) ⋯ ∝ p ( y ) ∏ i = 1 n p ( X i ∣ y )
\begin{aligned}
p(y|X_1,X_2, \cdots,X_n) \\
&\propto p(y, X_1,X_2, \cdots,X_n) \\
&\propto p(y)p(X_1|y)p(X_2|y)p(X_3|y) \cdots \\
&\propto p(y)\prod_{i=1}^{n}p(X_i|y)
\end{aligned}
p ( y ∣ X 1 , X 2 , ⋯ , X n ) ∝ p ( y , X 1 , X 2 , ⋯ , X n ) ∝ p ( y ) p ( X 1 ∣ y ) p ( X 2 ∣ y ) p ( X 3 ∣ y ) ⋯ ∝ p ( y ) i = 1 ∏ n p ( X i ∣ y )
所以这意味着,类变量 y y y
p ( y ∣ X 1 , X 2 , ⋯ , X n ) = 1 Z p ( y ) ∏ i = 1 n p ( X i ∣ y ) p(y|X_1,X_2, \cdots,X_n) = \frac{1}{Z}p(y)\prod_{i=1}^{n}p(X_i|y) p ( y ∣ X 1 , X 2 , ⋯ , X n ) = Z 1 p ( y ) i = 1 ∏ n p ( X i ∣ y )
其中 Z Z Z X 1 , X 2 , ⋯ , X n X_1,X_2, \cdots,X_n X 1 , X 2 , ⋯ , X n (prior) p ( y ) p(y) p ( y ) p ( X i ∣ y ) p(X_i|y) p ( X i ∣ y ) ∏ i = 1 n p ( X i ∣ y ) \prod_{i=1}^{n}p(X_i|y) ∏ i = 1 n p ( X i ∣ y ) (likelihood) 上述模型概率的稳定性得到很大提升。
第三部分:从概率模型中构造分类器 那么如何从朴素贝叶斯概率模型来构造一个分类器,这需要建立一个决策法则,一个很常见的法则就是选出最有可能的那个,就是最大后验概率(MAP) 决策准则,相应的分类器是如下定义的公式,这里我们假设 y y y K K K k k k
y ^ = arg max k ∈ [ 1 , ⋯ , K ] p ( y k ) ∏ i = 1 n p ( X i ∣ y k ) \hat y = \argmax\limits_{k \in [1,\cdots,K]}p(y_k)\prod_{i=1}^{n}p(X_i|y_k) y ^ = k ∈ [ 1 , ⋯ , K ] a r g m a x p ( y k ) i = 1 ∏ n p ( X i ∣ y k )
所有的模型参数都可以通过训练集的相关频率来估计,类的先验概率可以通过假设各类等概率来计算先 验 概 率 = 1 类 的 数 量 先验概率 = \frac{1} {类的数量} 先 验 概 率 = 类 的 数 量 1 A 类 先 验 概 率 = A 类 样 本 的 数 量 样 本 总 数 A类先验概率=\frac{A类样本的数量}{样本总数} A 类 先 验 概 率 = 样 本 总 数 A 类 样 本 的 数 量
延伸:高斯朴素贝叶斯(GBN),线性判别分析(LDA),二次判别分析(QDA) 第一部分:高斯朴素贝叶斯(GBN)
如果要处理的是连续 数据,一种通常的假设是这些连续数值为高斯分布 。 例如,假设训练集中有一个连续特征 x x x x x x 均值 和方差 。
我们有:
p ( y = k ∣ X = x ) = π k f k ( x ) ∑ l = 1 k π l f l ( x ) p(y=k|X=x)=\frac{\pi_kf_k(x)}{\sum_{l=1}^{k}\pi_lf_l(x)} p ( y = k ∣ X = x ) = ∑ l = 1 k π l f l ( x ) π k f k ( x )
其中 π k \pi_k π k 先验概率 (prior),f k ( x ) f_k(x) f k ( x ) 似然函数 (likelihood)。
我们用一个特征 x = v x=v x = v
p ( x = v ∣ y = k ) = f k ( x ) = 1 2 π σ y 2 e x p ( − ( v − μ y ) 2 2 σ y 2 ) p(x = v|y=k) =f_k(x)= \frac{1}{\sqrt{2\pi\sigma_y^2}}exp\Big(-\frac{(v-\mu_y)^2}{2\sigma_y^2}\Big) p ( x = v ∣ y = k ) = f k ( x ) = 2 π σ y 2 1 e x p ( − 2 σ y 2 ( v − μ y ) 2 )
处理连续数值问题的另一种常用的技术是通过离散化连续数值的方法。通常,当训练样本数量较少 或者是精确的分布已知 时,通过概率分布的方法是一种更好的选择。在大量样本的情形下离散化的方法表现更优,因为大量的样本可以学习到数据的分布。由于朴素贝叶斯是一种典型的用到font color=red>大量样本的方法(越大计算量的模型可以产生越高的分类精确度 ),所以朴素贝叶斯方法都用到离散化方法,而不是概率分布估计的方法。
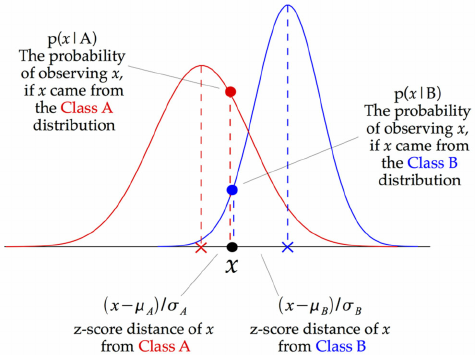
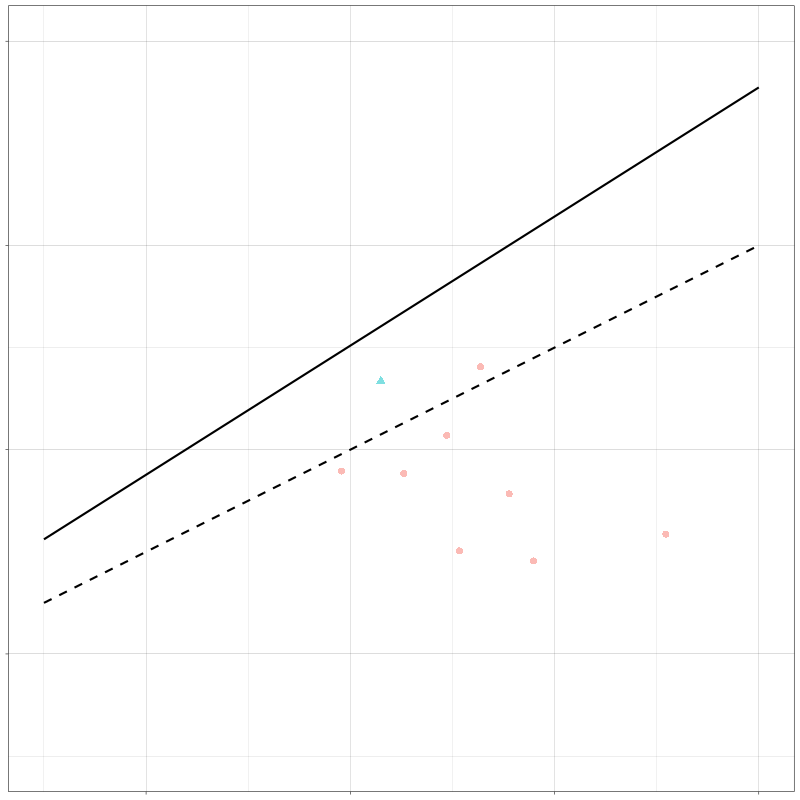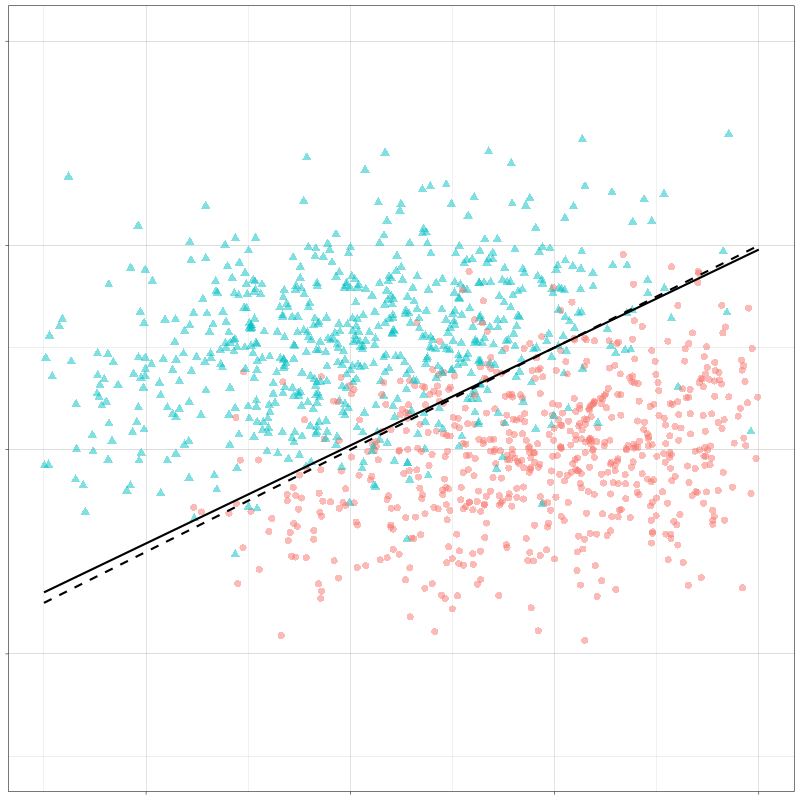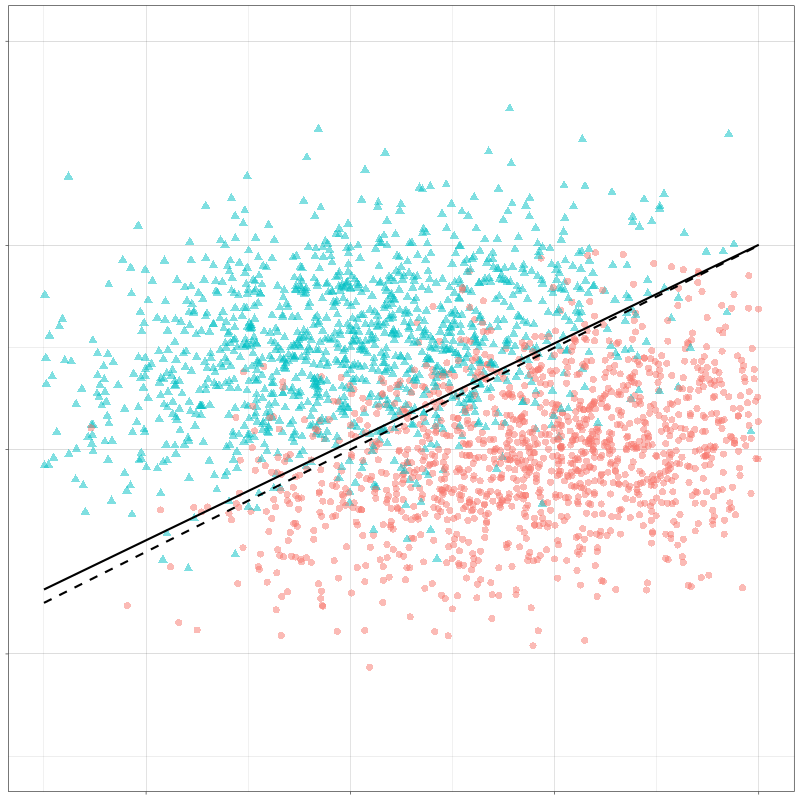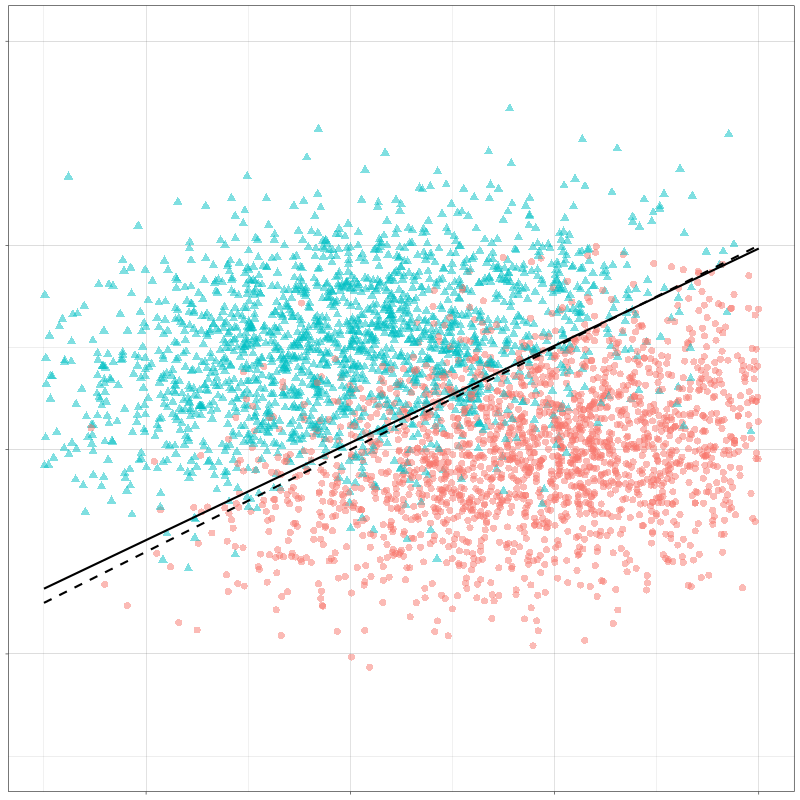
下面是GBN分类器的工作原理,在每一个数据点,在这一点和每个类平均(class-mean)的z-score都可以被计算出来。
如果一个给定的类和特征值在训练集中没有一起出现过,那么基于频率的估计下该概率将为0。这将是一个问题。因为与其他概率相乘时将会把其他概率的信息统统去除。所以常常要求要对每个小类样本的概率估计进行修正,以保证不会出现有为0的概率出现。
尽管实际上独立假设常常是不准确的,但朴素贝叶斯分类器的若干特性让其在实践中能够获取令人惊奇的效果。特别地,各类条件特征之间的解耦 (数学中解耦是指使含有多个变量的数学方程变成能够用单个变量表示的方程组,即变量不再同时共同直接影响一个方程的结果,从而简化分析计算)意味着每个特征的分布都可以独立地被当做一维分布来估计。
这样减轻了由于维数灾难 带来的阻碍,当样本的特征个数增加时就不需要使样本规模呈指数增长。然而朴素贝叶斯在大多数情况下不能对类概率做出非常准确的估计,但在许多应用中这一点并不要求。
例如,朴素贝叶斯分类器中,依据最大后验概率决策规则只要正确类的后验概率比其他类要高就可以得到正确的分类。所以不管概率估计轻度的甚至是严重的不精确都不影响正确的分类结果。在这种方式下,分类器可以有足够的鲁棒性去忽略朴素贝叶斯概率模型上存在的缺陷。
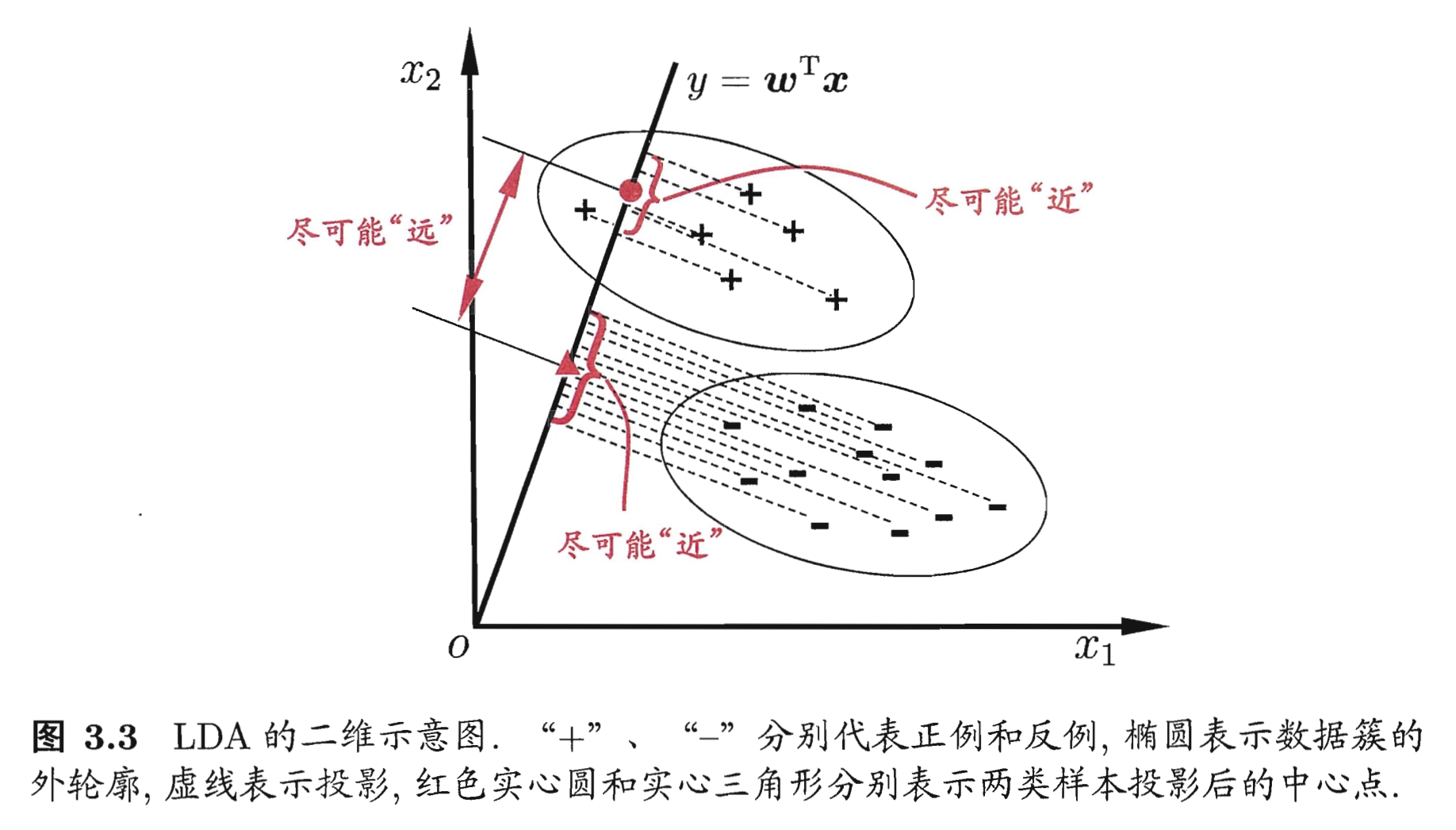
第二部分:线性判别分析(LDA) LDA核心思想 LDA作为一种有监督学习的降维、分类技术,可以在保持分类的前提下把数据投影到低维空间以降低计算复杂度。
LDA要求类间的方差最大,而类内的方差最小 ,以保证投影后同一分类数据集中,不同分类间数据距离尽可能大。
LDA数学推导 回顾一下之前说过的朴素贝叶斯方法,我们有:
P r i o r s = p ( y = k ) = π k Priors = p(y=k) = \pi_k P r i o r s = p ( y = k ) = π k L i k e l i h o o d = p ( X = x ∣ y = k ) = f k ( x ) = 1 ( 2 π ) n / 2 ∣ Σ ∣ 1 / 2 e x p ( − 1 2 ( x − μ k ) T Σ − 1 ( x − μ k ) ) Likelihood = p(X=x|y=k)=f_k(x)=\frac{1}{(2\pi)^{n/2}|\Sigma|^{1/2}}exp(-\frac{1}{2}(x-\mu_k)^T\Sigma^{-1}(x-\mu_k)) L i k e l i h o o d = p ( X = x ∣ y = k ) = f k ( x ) = ( 2 π ) n / 2 ∣ Σ ∣ 1 / 2 1 e x p ( − 2 1 ( x − μ k ) T Σ − 1 ( x − μ k ) ) μ k \mu_k μ k k k k Σ \Sigma Σ (Common to all categories) 十分重要的假设,我们假设对每一类数据的协方差矩阵是相等的!
根据贝叶斯公式,我们计算出后验概率:
p ( y = k ∣ X = x ) = f k ( x ) π k P ( X = x ) p(y=k|X=x)=\frac{f_k(x)\pi_k}{P(X=x)} p ( y = k ∣ X = x ) = P ( X = x ) f k ( x ) π k
同样,分母可看做常数
p ( y = k ∣ X = x ) = C × f k ( x ) π k p(y=k|X=x)=C\times{f_k(x)\pi_k} p ( y = k ∣ X = x ) = C × f k ( x ) π k
展开可得
p ( y = k ∣ X = x ) = C π k ( 2 π ) n / 2 ∣ Σ ∣ 1 / 2 e x p ( − 1 2 ( x − μ k ) T Σ − 1 ( x − μ k ) ) p(y=k|X=x)=\frac{C\pi_k}{(2\pi)^{n/2}|\Sigma|^{1/2}}exp(-\frac{1}{2}(x-\mu_k)^T\Sigma^{-1}(x-\mu_k)) p ( y = k ∣ X = x ) = ( 2 π ) n / 2 ∣ Σ ∣ 1 / 2 C π k e x p ( − 2 1 ( x − μ k ) T Σ − 1 ( x − μ k ) )
下面,我们把与 k k k C ′ C' C ′
p ( y = k ∣ X = x ) = C ′ π k e − 1 2 ( x − μ k ) T Σ − 1 ( x − μ k ) p(y=k|X=x)=C'\pi_ke^{-\frac{1}{2}(x-\mu_k)^T\Sigma^{-1}(x-\mu_k)} p ( y = k ∣ X = x ) = C ′ π k e − 2 1 ( x − μ k ) T Σ − 1 ( x − μ k )
下面,对等式两边取对数
l o g p ( y = k ∣ X = x ) = l o g C ′ + l o g π k − 1 2 ( x − μ k ) T Σ − 1 ( x − μ k ) log\ p(y=k|X=x)=log\ C'+log\ \pi_k-\frac{1}{2}(x-\mu_k)^T\Sigma^{-1}(x-\mu_k) l o g p ( y = k ∣ X = x ) = l o g C ′ + l o g π k − 2 1 ( x − μ k ) T Σ − 1 ( x − μ k )
注意,l o g C ′ log\ C' l o g C ′ k k k k k k
T a r g e t = l o g π k − 1 2 ( x − μ k ) T Σ − 1 ( x − μ k ) = l o g π k − 1 2 [ x T Σ − 1 x + μ k T Σ − 1 μ k ] + x T Σ − 1 μ k = C ′ ′ + l o g π k − 1 2 μ k T Σ − 1 μ k + x T Σ − 1 μ k
\begin{aligned}
Target &= log\ \pi_k-\frac{1}{2}(x-\mu_k)^T\Sigma^{-1}(x-\mu_k) \\
&= log\ \pi_k-\frac{1}{2}[x^T\Sigma^{-1}x+\mu_k^T\Sigma^{-1}\mu_k]+x^T\Sigma^{-1}\mu_k \\
&= C''+log\ \pi_k - \frac{1}{2}\mu_k^T\Sigma^{-1}\mu_k+x^T\Sigma^{-1}\mu_k
\end{aligned}
T a r g e t = l o g π k − 2 1 ( x − μ k ) T Σ − 1 ( x − μ k ) = l o g π k − 2 1 [ x T Σ − 1 x + μ k T Σ − 1 μ k ] + x T Σ − 1 μ k = C ′ ′ + l o g π k − 2 1 μ k T Σ − 1 μ k + x T Σ − 1 μ k
我们定义我们要最大化的目标函数
δ k ( x ) = l o g π k − 1 2 μ k T Σ − 1 μ k + x T Σ − 1 μ k \delta_k(x) = log\ \pi_k-\frac{1}{2}\mu_k^T\Sigma^{-1}\mu_k+x^T\Sigma^{-1}\mu_k δ k ( x ) = l o g π k − 2 1 μ k T Σ − 1 μ k + x T Σ − 1 μ k
通过最大化 δ k ( x ) \delta_k(x) δ k ( x ) x x x
下面来看看LDA的决策边界
什么是决策边界?也就是一系列的数据点使得:
δ k ( x ) = δ l ( x ) \delta_k(x) = \delta_l(x) δ k ( x ) = δ l ( x )
l o g π k − 1 2 μ k T Σ − 1 μ k + x T Σ − 1 μ k = l o g π k − 1 2 μ l T Σ − 1 μ l + x T Σ − 1 μ l log\ \pi_k-\frac{1}{2}\mu_k^T\Sigma^{-1}\mu_k+x^T\Sigma^{-1}\mu_k = log\ \pi_k-\frac{1}{2}\mu_l^T\Sigma^{-1}\mu_l+x^T\Sigma^{-1}\mu_l l o g π k − 2 1 μ k T Σ − 1 μ k + x T Σ − 1 μ k = l o g π k − 2 1 μ l T Σ − 1 μ l + x T Σ − 1 μ l
那么接下来就到了参数估计的步骤了,记得之前我们已经说过 π k \pi_k π k μ k \mu_k μ k Σ \Sigma Σ
μ ^ k = 1 # ( i ; y i = k ) ∑ i ; y i = k x i \hat\mu_k = \frac{1}{\#(i;y_i=k)}\sum_{i;y_i=k}x_i μ ^ k = # ( i ; y i = k ) 1 i ; y i = k ∑ x i
σ ^ 2 = 1 n − K ∑ k = 1 K ∑ i ; y i = k ( x i − μ ^ k ) 2 \hat\sigma^2=\frac{1}{n-K}\sum_{k=1}^{K}\sum_{i;y_i=k}(x_i-\hat\mu_k)^2 σ ^ 2 = n − K 1 k = 1 ∑ K i ; y i = k ∑ ( x i − μ ^ k ) 2
这里的 ∑ i ; y i = k \sum_{i;y_i=k} ∑ i ; y i = k k k k
X = ( X 1 , X 2 , ⋯ , X n ) X = (X_1,X_2,\cdots,X_n) X = ( X 1 , X 2 , ⋯ , X n ) X ∼ N ( μ , Σ ) X \sim N(\mu,\Sigma) X ∼ N ( μ , Σ )
所以根据我们之前推出的 δ k ( x ) \delta_k(x) δ k ( x )
δ ^ k ( x ) = l o g π ^ k − 1 2 μ ^ k T Σ ^ − 1 μ ^ k + x T Σ ^ − 1 μ ^ k \hat\delta_k(x) = log\ \hat\pi_k-\frac{1}{2}\hat\mu_k^T\hat\Sigma^{-1}\hat\mu_k+x^T\hat\Sigma^{-1}\hat\mu_k δ ^ k ( x ) = l o g π ^ k − 2 1 μ ^ k T Σ ^ − 1 μ ^ k + x T Σ ^ − 1 μ ^ k
LDA与逻辑回归的关系
首先LR对于可以类别可以很准确分类的情况(well-seperated)很不稳定,而且很难处理多类分类问题,所以LDA作为一个生成模型,针对那些 f ( X ∣ y ) f(X|y) f ( X ∣ y )
对于LR,我们有p ( y = 1 ∣ X ) = p 1 = 1 1 + e − θ T x p(y=1|X)=p_1=\frac{1}{1+e^{-\theta^Tx}} p ( y = 1 ∣ X ) = p 1 = 1 + e − θ T x 1 l o g ( p 1 1 − p 1 ) = θ T x log(\frac{p_1}{1-p_1})=\theta^Tx l o g ( 1 − p 1 p 1 ) = θ T x l o g ( p 1 1 − p 1 ) = w T x log(\frac{p_1}{1-p_1})=w^Tx l o g ( 1 − p 1 p 1 ) = w T x w w w μ k \mu_k μ k σ k \sigma_k σ k
第三部分:二次判别分析(QDA) 至于QDA,它跟LDA的区别在于我们去掉了之前重要的假设,也就是在QDA中,我们要对每个类 k k k μ ^ k \hat\mu_k μ ^ k Σ ^ k \hat\Sigma_k Σ ^ k
根据之前推导的 δ k ( x ) \delta_k(x) δ k ( x )
δ k ( x ) = l o g π k − 1 2 μ k T Σ − 1 μ k + x T Σ − 1 μ k − 1 2 x T Σ k − 1 x − 1 2 l o g ∣ Σ k ∣ \delta_k(x) = log\ \pi_k-\frac{1}{2}\mu_k^T\Sigma^{-1}\mu_k+x^T\Sigma^{-1}\mu_k - \frac{1}{2}x^T\Sigma_k^{-1}x-\frac{1}{2}log\ |\Sigma_k| δ k ( x ) = l o g π k − 2 1 μ k T Σ − 1 μ k + x T Σ − 1 μ k − 2 1 x T Σ k − 1 x − 2 1 l o g ∣ Σ k ∣
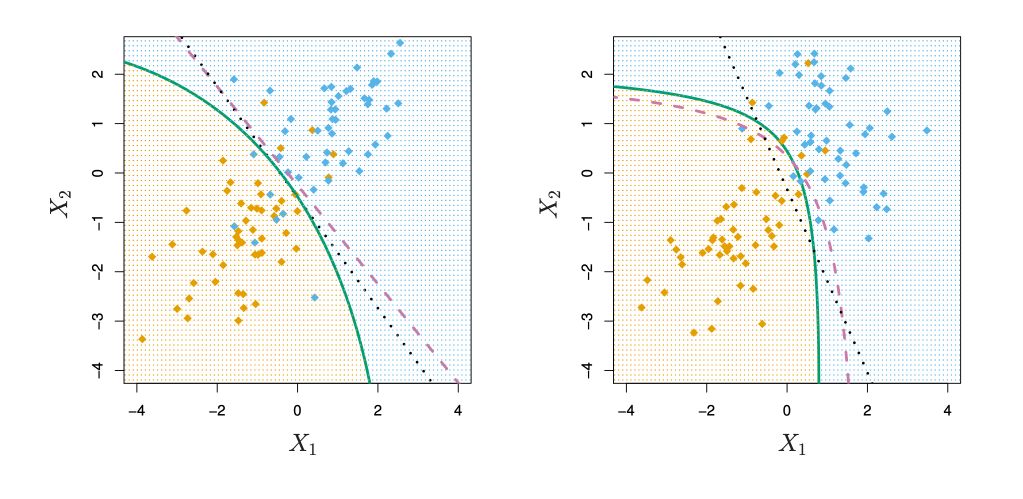
可以看出 δ k ( x ) \delta_k(x) δ k ( x ) x x x 二次函数
来看一下LDA和QDA的决策边界的对比
当我们分别去求 Σ ^ k \hat\Sigma_k Σ ^ k
实际应用和代码展示 朴素贝叶斯方法相关面经和其他资料 小结 朴素贝叶斯算法的基本思想是建立特征 X X X y y y p ( X , y ) p(X,y) p ( X , y ) 贝叶斯定理 求出所有可能的输出 p(X|y) ,取其中最大的作为预测结果。其优点是模型简单,效率高,在很多领域有广泛的使用。朴素贝叶斯、LDA/QDA都属于生成模型,收敛速度将快于判别模型(如逻辑回归)。