逻辑回归

• 什么是逻辑回归
• 核心思想（1）：Sigmoid函数
• 核心思想（2）：极大似然估计（MLE）、损失函数
• 核心思想（3）：梯度下降法
• 实际应用和代码展示
• 逻辑回归面经和其他资料
• 小结

逻辑回归是什么？为什么要引入？

一句话概括：逻辑回归假设数据服从伯努利分布，通过极大似然化函数的方法，运用梯度下降来求解参数，从而达到二分类的目的。

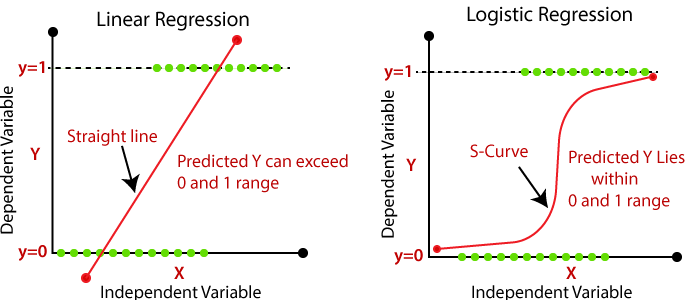
首先逻辑回归虽名为回归，但并不是一个回归方法，它主要用来解决二分类问题，面对分类问题，上文的线性回归显得无能为力，从下图可以看到，线性回归在对作为离散变量存在的y时，只能用直线进行拟合，并且所预测的y可能会超过0到1的范围，并且对异常值非常敏感。

那么我们想引入非线性元素，来解决以上两个问题，我们希望输出的值$p(y=1|X;\theta)$保证在 $0$ 到 $1$ 之间，并且对异常值不在敏感。

对一个二分类问题，我们假设：

$Predict=\left\{ \begin{array}{rcl} 1 & & {if \space h_\theta(x) \geqslant0.5}\\ 0 & & {if \space h_\theta(x)<0.5} \end{array} \right.$

这里的$h_\theta(x)$跟前面定义的一样，是$\theta^TX$，相当于所有特征的线性组合，当然这里的0.5并不是绝对的，我们只是常用0.5来作为一个门槛，来界定如何分类。

那么我们如何引入非线性因素来完成二分类任务呢？

核心思想：Sigmoid函数、极大似然估计、损失函数（包含理论推导）

第一部分：Sigmoid函数

我们利用判别模型来对 $p(y=1|X;\theta)$ 建模，利用贝叶斯定理：

$p(y=1|X;\theta) = \frac{p(X;\theta|y=1) p(y=1)}{p(X;\theta|y=1) p(y=1)+p(X;\theta|y=0) p(y=0)}$
取$a = ln\frac{p(X;\theta|y=1) p(y=1)}{p(X;\theta|y=0) p(y=0)}$，于是：

$p(y=1|X;\theta) = \frac{1}{1+exp(-a)}$

上面的公式就是所谓的Sigmoid函数，图像如下：

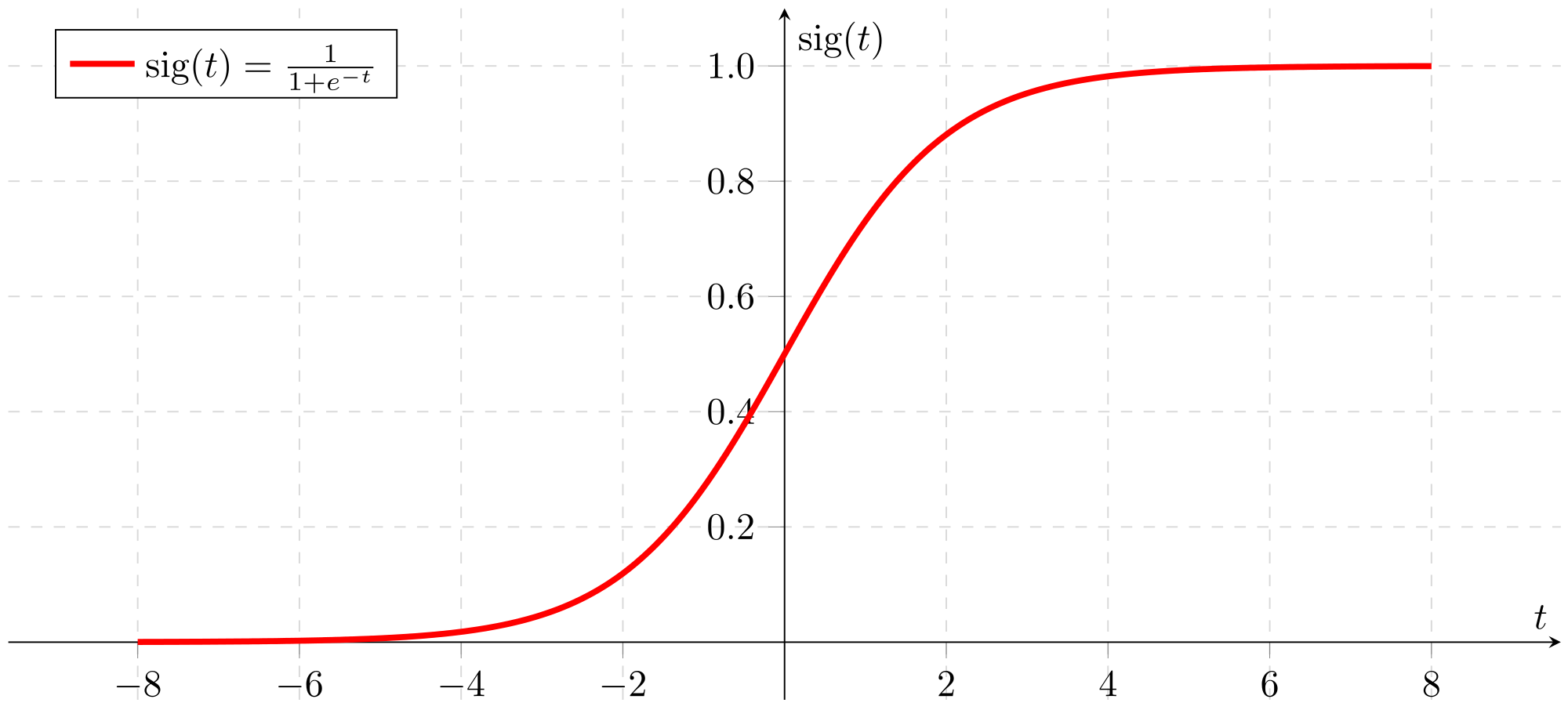
其中的参数表示了两类联合概率比值的对数，我们并不关心这个参数的具体值，因为我们可以关于模型直接对$a$假设：
$a = \theta^TX$

所以，Sigmoid函数就变为了

$p(y=1|X;\theta) = \frac{1}{1+e^{-\theta^TX}}=h_\theta(x)=p_1$

于是，问题便转化成了找 $\theta$ 的最佳值从而最优化模型，但是怎么衡量模型的好坏呢？也就引出了所谓的损失函数，我们不断优化参数来最小化损失函数，找到最优的参数，那么概率判别模型常用最大似然估计（MLE）的方法来确定参数。

第二部分：极大似然估计（MLE）、损失函数

之前总结过，我们假设数据服从伯努利分布，什么是伯努利分布？

伯努利试验是单次随机试验，只有 成功（值为1）或 失败（值为0） 这两种结果，在这里也就是随机抽取一个数据点，不是属于第一类（$y=1$）就是属于第二类（$y=0$）的情况，所以对于一次观测，得到分类y的概率是

$p(y|x;\theta)=p_1^y(1-p_1)^{(1-y)}$

这里 $y=1$ 或者 $0$，所以对于$N$次独立的观测，每一个观测情况下， 我们有

$p(y_i|x_i;\theta)=h_\theta(x_i)^{y_i}(1-h_\theta(x_i))^{(1-y_i)}$

所以对于所有$N$个独立的观测值，我们有

$p(y|X;\theta)=\prod_{i=1}^{N}[h_\theta(x_i)^{y_i}(1-h_\theta(x_i))^{(1-y_i)}]=L(\theta)$

我们对等式两边同时取对数得到：

$l(\theta)=\sum_{i=1}^{N}[y_ilog(h_\theta(x_i))+(1-y_i)log(1-h_\theta(x_i))]$

从而我们要利用极大似然估计的方法得到：

$\hat\theta = arg\max\limits_{\theta}l(\theta)=arg\max\limits_{\theta}\sum_{i=1}^{N}[y_ilog(h_\theta(x_i))+(1-y_i)log(1-h_\theta(x_i))]$

这里我们发现，要最大化 $l(\theta)$ 来确定参数，那么最小化 $-l(\theta)$ 不就是相当于最小化损失函数了么？那么我们终于找到了所谓的损失函数了！

$\hat\theta = arg\min\limits_{\theta}J(\theta)=arg\min\limits_{\theta}-\sum_{i=1}^{N}[y_ilog(h_\theta(x_i))+(1-y_i)log(1-h_\theta(x_i))]$

这里的损失函数为：

$J(\theta)=-\frac{1}{N}\sum_{i=1}^{N}[y_ilog(h_\theta(x_i))+(1-y_i)log(1-h_\theta(x_i))]$

注意这里的$\frac{1}{N}$是个常数，用来归一化，对于上式中的最小化不影响，所以省略了。

那么我们继续刚才的推导，我们对于 $l(\theta)$ 关于 $\theta$ 求偏导数得到（我们以一个观测值为例）

$\frac{\partial l(\theta) }{\partial \theta} = \frac{y_i}{h_\theta(x_i)} \cdot \frac{\partial h_\theta(x_i)}{\partial \theta} + \frac{1-y_i}{1-h_\theta(x_i)} \cdot -\frac{\partial h_\theta(x_i)}{\partial \theta}$

注意到
$\frac{\partial h_\theta(x_i)}{\partial \theta} = x_ih_\theta(x_i)(1-h_\theta(x_i))$

如果不信的话，可以自己求一下下，比较简单，所以带入后最终结果为

$\frac{\partial l(\theta) }{\partial \theta} = \sum_{i=1}^{N}y_i(1-p_1)x_i-p_1x_i+y_ip_1x_i=\sum_{i=1}^{N}(y_i-p_1)x_i$

注意这里的 $p_1 = h_\theta(x_i)$，也就是给定数据和参数，使其分类为 $y=1$ 的概率，这个很重要，一定要搞清楚，记牢固！

思考：

为什么不想线性回归那样定义损失函数呢？在线性回归中，我们有

$J(\theta) = \frac{1}{N}\sum_{i=1}^{N}\frac{1}{2}(h_\theta(x_i)-y_i)^2$

但是如果我们把 $h_\theta(x_i) = \frac{1}{1+e^{-\theta^Tx_i}}$ 带入上式中，我们会发现这个函数不是凸函数（convex）了，如图所示：

因此我们采用MLE的方法来确定参数！

第三部分：梯度下降法

那么，我们知道对于逻辑回归，损失函数为（一个观测值为例）

$J(\theta) = \frac{1}{N}\sum_{i=1}^{N}Cost(h_\theta(x),y)$

这里的 $h_\theta(x)$ 为预测值，$y$ 为实际值，并且

$Cost(h_\theta(x),y) =\left\{ \begin{array}{rcl} -log(h_\theta(x)) & & {if \space y=1}\\ -log(1-h_\theta(x)) & & {if \space y=0} \end{array} \right.$

上面我们提到了要最小化损失函数，那么要利用到梯度下降法（Gradient Descent）

这里的 $\alpha$ 代表学习率，这个 $m$ 代表的就是带入模型的观测值数量（也可称做batch size，以后会讲），适当选取学习率和批大小对梯度下降的结果，也就是参数确定的结果有非常重要的影响！（后文会深入讨论）

当然，我们不光可以用梯度下降法来进行对损失函数的最小化，我们有多种optimization的选择，多种方法的速度和效率如下图所示：

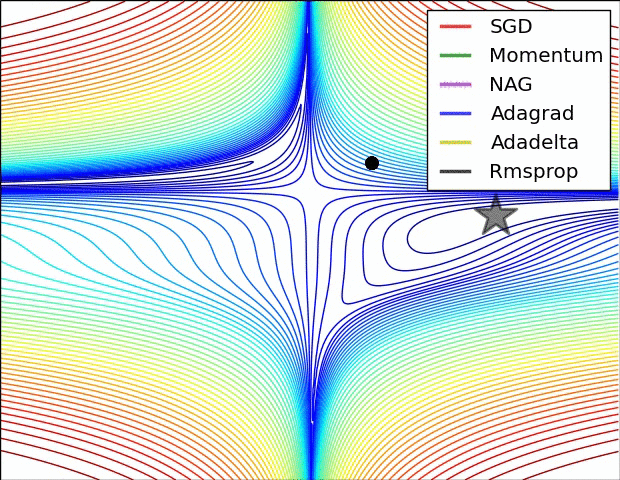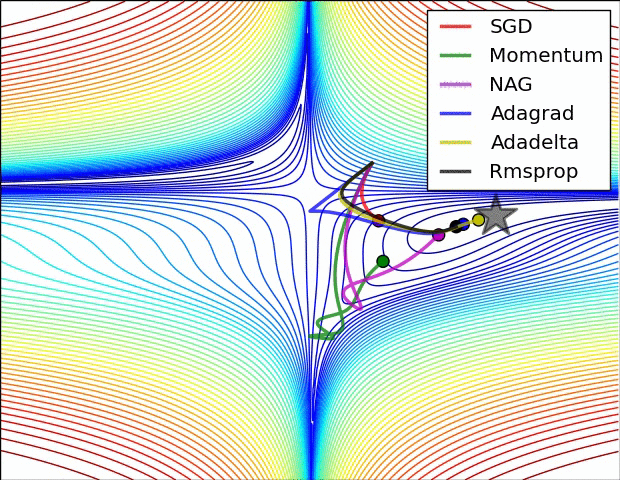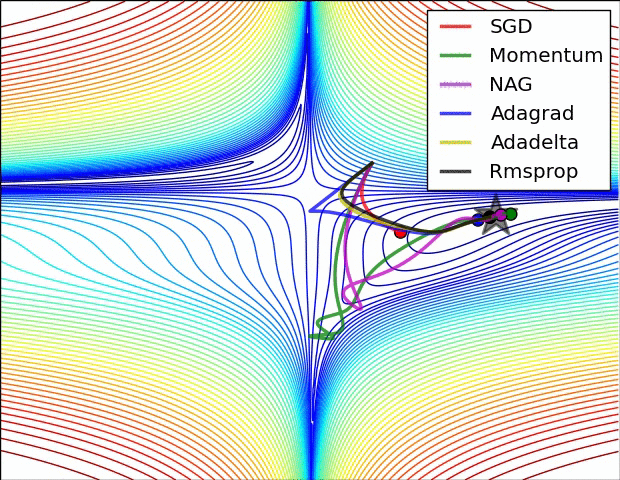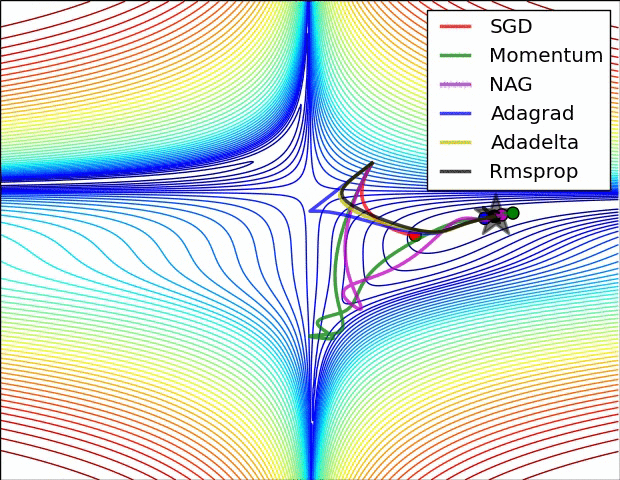
实际应用和代码展示

• Python
  • Titanic: logistic regression with python
  • Heart Disease Prediction using Logistic Regression
• R
  • Titanic - Logistic Regression in R
  • Intro to R Part 28: Logistic Regression

逻辑回归面经和其他资料

• 面经：

  • 逻辑回归面经整理——from牛客
  • 逻辑回归的常见面试点总结
  • 逻辑回归面试题汇总(整理)
  • 30 Questions to test your understanding of Logistic Regression

• 其他资料：

  • Logistic Regression by Christoph Molnar
  • 逻辑回归（Logistic Regression）详解
  • 快速掌握Logistic回归分析及应用
  • 逻辑回归总结-简书
  • 逻辑回归的优缺点总结
  • Mathematics vs. Coding in Basic Logistic Regression by Zijing
  • LR by Zijing

小结

逻辑回归模型是非常基础的二分类模型，也是我们接触更多机器学习算法的必经之路，在二分类问题上有非常优秀的表现，但同时也有一些缺点和局限性，比如对很依赖特征工程和特征选择（这个对于模型的结果十分重要！），容易欠拟合（模型复杂度不够），对分布很不均匀的数据效果不好等等，最重要的是，当某个或某些特征可以完全对目标类别进行分类时，逻辑回归会表现得很不稳定，也就是其中的 $p(Y=1|X;\theta) = 1$，那么 $ln(\frac{p(Y=1|X;\theta)}{1-p(Y=1|X;\theta)}) = \theta^TX$ 无解，系数会达到无穷，那么接下来我们引入生成模型，来探究其和判别模型的区别。