KNN

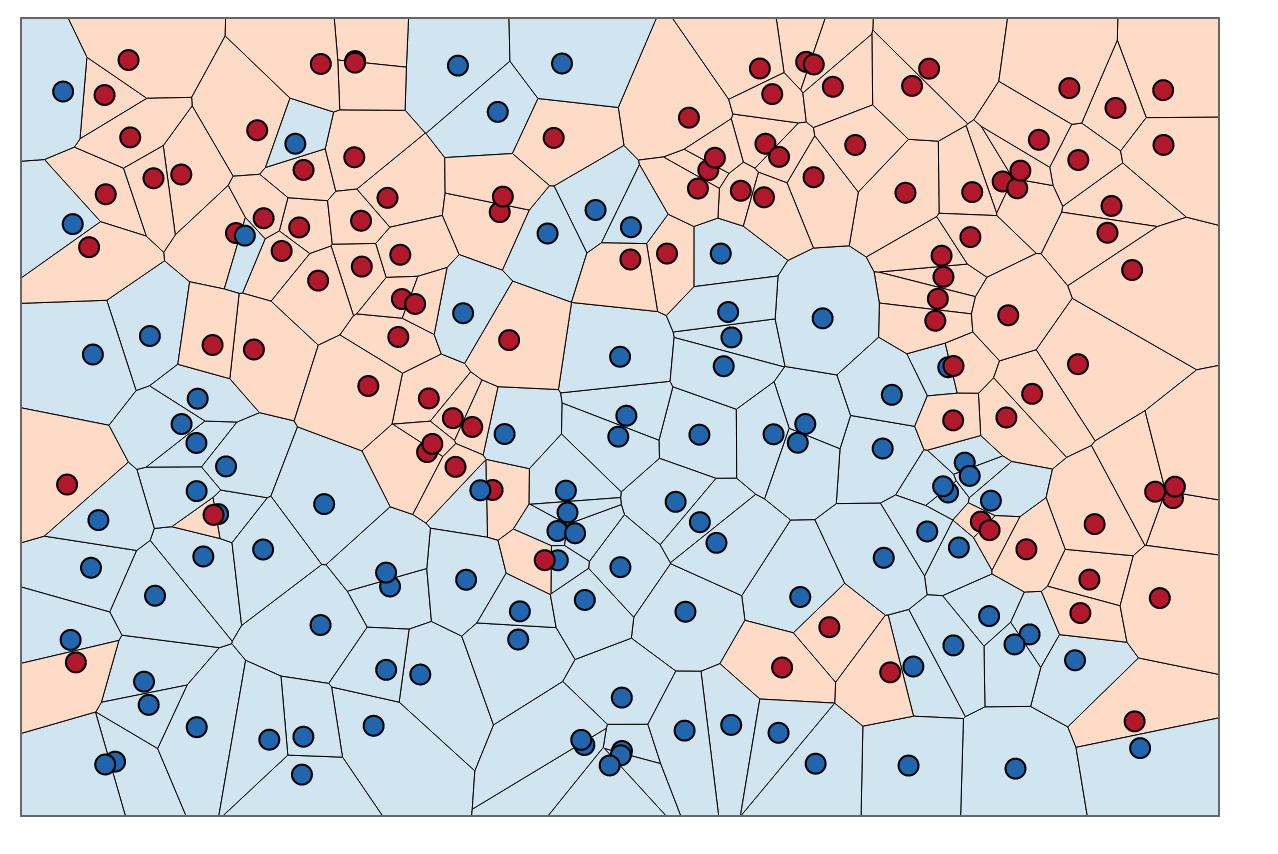
• 什么是 k 近邻算法
• 核心思想：K 近邻
• K的影响
• Python代码示例：Sklearn & Scratch
• KNN的优缺点
• 改进
• KNN面经和其他资料
• 小结

什么是 k 近邻算法

我们都已经熟悉了用 $X$ 来表示特征（feature）和 $y$ 来表示目标（target），KNN 作为一个监督性学习算法，也就是我们有一个带有目标结果的数据集 (X,y)，并且我们想要研究他们其中的关系，也就是习得一个方程 $h(x)$ 从而能用 $X$ 来预测 $y$。

$h: X \rarr y$

KNN 分类器也是一种 non parametric 并且 instance-based 算法.

• Non-parametric 说明它没有对函数 $h$ 做出任何明确的假设，从而避免了对数据的分布进行错误建模的危险。例如，假设我们的数据是高度非高斯分布的，但是我们选择的学习模型采用高斯形式（LDA），那么结果将会非常不如人意。
• Instance-based 说明我们的算法没有真正的学习模型。而是选择记忆所训练的实例，随后将其用作预测阶段的 “知识”。具体来说，这意味着仅当对我们的数据库进行查询时（即当我们要求它预测给定输入的标签时），该算法才会使用训练的实例给出答案。

值得注意的是，KNN的最小的训练阶段不仅要花费一个 “内存成本”（因为我们必须在测试期间存储一个巨大数据集）还要一个**“计算成本”**（因为对给定观察值进行分类需要消耗整个数据组）。实际上，这是不可取的。

核心思想：K 近邻

在进行分类时，K近邻算法本质上归结为在给定 “看不见” 的 K 个最相似实例之间根据少数服从多数来表决（所以也称为投票算法）。

如何定义相似度呢？我们根据两个数据点之间的距离度量来定义相似性。经常选用欧几里得距离来定义：

$d(x, x') = \sqrt{\left(x_1 - x'_1 \right)^2 + \dotsc + \left(x_n - x'_n \right)^2}$

但是也有其他的选择例如：Manhattan、Chebyshev以及Hamming 距离。

给定一个正整数 K、一个未知的观测值 $x$ 和一个衡量具体的方法 $d$，KNN 通过下列步骤进行分类：

• 它跑遍整个数据集计算 $x$ 和每个训练集观测值之间的距离。我们将训练数据集中最接近 $x$ 的 K 个点称为集合 $A$。注意，为了防止出现平局情况，K 通常是奇数。

• 接下来，它估计每个类别的条件概率，即具有给定类别标签的集合 $A$ 中点的比例。（注意 $I(x)$ 是个 indicator 函数，其参数 $x$ 为 true 时返回 1，否则为 0）

$P(y = j | X = x) = \frac{1}{K} \sum_{i \in \mathcal{A}} I(y^{(i)} = j)$

最后，我们输入的 $x$ 根据最大的概率被分到对应的类别中。

KNN searches the memorized training observations for the K instances that most closely resemble the new instance and assigns to it the their most common class.

K的影响

那么现在，KNN 算法你应该了解了，但是关于 K 的选取还是很重要的，类似于其他的机器学习算法，K 是一个超参数，是用来控制决策边界的形状的。

当 K 较小时，我们将 “眼光” 局限在给定预测的区域，并对我们的分类器对整体分布“视而不见”，它将具有低偏差但高方差的性质（也就是overfitting）。在图形上，决策边界将更加参差不齐。

另一方面，较大的 K 表示每个预测情况中的平均 “选民” 更多（也就是我们更偏重全局的考虑，每次考虑的数据点更多，模型有更强的泛化能力），因此对异常值的适应性更高。较大的 K 值将具有较平滑的决策边界，这意味着方差较小，但偏差增加（K 过大会 underfitting）

KNN的优缺点

• 优点

  • 简单易懂
  • 没有数据分布的假设条件
  • 对多类别分类的情况一样好用

• 缺点

  • 计算量大，大数据情况使用起来效率低
  • 对于偏分布的数据效果很差，假如一类数据出现频率极高，就会严重压制其他类别，在投票时，我们就会忽略他们的存在
  • 高维数据表现不好，高维情况下，距离的远近变得模糊

改进

• 改进偏分布的一种简单有效的方法是用 “加权投票”（weighed voting）。 K个邻居中每个邻居的类别乘以与从该点到给定测试点的距离的倒数成比例的权重。这确保了较近的邻居比较远的邻居对最终投票的贡献更大
• 改变衡量距离的方法
• 对**数据归一化（normalize）**使距离的概念更明显
• 降维
• 近似最近邻（例如使用 k-d树 存储训练观测值）可用于减少测试时间。但是这个方法在高维（20+）上往往表现不佳。如果维度过高，可尝试用区域敏感哈希（LHS）。

KNN面经和其他资料

• 面经

  • 30 Questions to test a data scientist on K-Nearest Neighbors (kNN) Algorithm
  • Interview Case Study #1: The Statistics Of KNN Parameter Optimization
  • KNN面经

• 其他资料

  • Stanfords CS231n notes on KNN
  • Scikit-learn’s documentation for KNN
  • KNN小结-刘建平

小结

K近邻法（k-nearest neighbors,KNN）是一种很基本的机器学习方法了，在我们平常的生活中也会不自主的应用。比如，我们判断一个人的人品，只需要观察他来往最密切的几个人的人品好坏就可以得出了。这里就运用了KNN的思想。KNN方法既可以做分类，也可以做回归，这点和决策树算法相同。