VAE 理论基础¶
简介¶
变分自编码器(VAE)是一个生成模型(generative model),于2013年由 Diederik P.Kingma 和 Max Welling 提出。
之前讲过了 Auto-encoder,也就是自编码器,那么自编码器是使用编码层来把数据压缩得到低维的隐向量,再用解码器生成数据,也即是把低维的向量重构,并最小化重构误差。
不过,AE 只能简单地记住数据,生成数据的能力较,但是通过 VAE,我们就可以从标准正态分布生成数据作为解码器的输入,来生成类似但不同于训练数据的新样本,具有更强的生成能力。
特点¶
传统的自编码器有以下特点:
- 自动编码器是数据相关的(data-specific 或 data-dependent),这意味着自动编码器只能压缩那些与训练数据类似的数据。比如,使用人脸训练出来的自动编码器在压缩别的图片,比如树木时性能很差,因为它学习到的特征是与人脸相关的。
- 自动编码器是有损的,意思是解压缩的输出与原来的输入相比是退化的,MP3,JPEG等压缩算法也是如此。这与无损压缩算法不同。
- 自动编码器是从数据样本中自动学习的,这意味着很容易对指定类的输入训练出一种特定的编码器,而不需要完成任何新工作。
相比之下,VAE 在生成数据的能力上要强很多,其实现过程如下:
其实和 AE 相比,编码和解码过程都不变,只不过在中间加入了一些小技巧,我们通过 AE 还不能产生任何未知的东西,因为我们不能随意产生合理的潜在变量,所以我们要对编码器添加约束,也就是强迫它服从单位高斯分布的潜在变量。那么产生新的图片也很容易,我们只要从单位高斯分布中采样,然后传给 decoder 即可。

如上图所示,我们把原图像映射成为正态分布的两个参数(均值和标准差)而不是直接映射成为隐向量,也就是传统的 encoder 变成了 probabilistic encoder,那么具体应该怎么做呢?训练过程中,为了生成样本 $z$ 以便于 decoder 操作,我们可以从 encoder 生成的分布中进行采样。但是,由于反向传播无法通过随机节点,所以这样操作不可取,为了解决这个问题,我们用了重参数化技巧(Reparameterization Trick)。使用 $ z = \mu + \sigma \odot \epsilon, ~~~~ \epsilon \sim N(0,I)$ 对其转换,其中 $\mu$ 和 $\sigma$ 表示高斯分布中的均值和标准差,而 $\epsilon$ 用来保持 $z$ 随机性的随机噪声,从标准正态分布中生成,再作为输入丢进解码器里面最终完成重构。
补充:那么为什么反向传播不能通过随机节点?
因为采样的操作是不可导的,而采样的结果是可导的。所以我们利用
$$\begin{aligned} \frac{1}{\sqrt{2 \pi \sigma^2}} \exp \Bigg( - \frac{(z-\mu)^2}{2\sigma^2}\Bigg) dz = \frac{1}{\sqrt{2 \pi}} \exp \Bigg( -\frac{1}{2} \frac{(z-\mu)^2}{\sigma^2} \Bigg) d\big(\frac{z-\mu}{\sigma}\big) \end{aligned}$$可以发现,$(z−\mu)/\sigma=\epsilon$ 是服从均值为 0,方差为 1 的标准正态分布的!因此,我们发现,从 $N(\mu,\sigma^2)$ 中采样一个 $z$,相当于从 $N(0,I)$ 中采样一个 $\epsilon$,然后让 $ z = \mu + \sigma \odot \epsilon$。通常我们把这一步称为“重参数技巧”。经过Reparametrization之后,将随机性转移到变量 $\epsilon$ 上面( $\epsilon$ 的前驱节点没有我们需要梯度回传的地方,因此可以放心对其建模为随机节点)

原理¶

上图是VAE的图模型。我们能观测到的数据 $x$,而 $x$ 由隐变量 $z$产生,由 $z \rightarrow x$ 是生成模型 $p_\theta(x|z)$,从自编码器(auto-encoder)的角度来看,就是解码器;而由 $x \rightarrow z$ 是识别模型(recognition model)$q_\phi(z|x)$,类似于自编码器的编码器。
VAE 现在广泛地用于生成图像,当生成模型 $p_\theta(x|z)$ 训练好了以后,我们就可以用它来生成图像了。
实例¶

所以对于上图中的图像,AE 始终只能有一个输出,因为它的潜变量 $z$ (latent variable)永远不变,而 VAE 实际上在找潜变量的时候并不是一个确定的值,而是一个基于 $\mu$ 和 $\sigma$ 的一个概率分布。因此,由于潜在变量不同,对于同一张图片的输入,我们生成的结果可能并不是一样的。
那么既然潜在变量遵循高斯分布,当我们固定其他变量时,仅仅增加或者减少单个潜在变量,图片的生成效果变得很平滑。

当我们在训练中有许多不同的潜在变量,当然,理想情况下我们希望这些潜在变量都是独立互不相干的,以便我们可以沿着我们固定的维度上走,观察到不同的表达。如图,这有两个潜在变量,一个是笑容,另一个是头的角度,我们完全可以做到通过扰动这两个数字完成微笑和头的角度的自定义。
数学推导¶
先回顾一下变分推断,在概率图模型里面,我们经常假设观测变量为 $X$,隐变量为 $Z$,图模型的结构是由 $Z$ 生成 $X$。那么建立联合分布为:
$$p(X,Z) = p(X|Z)p(Z)$$为了计算观测变量 $X$ 的对数似然 $\ln p(X)$,一般来说要将隐变量积分掉,即:
$$\ln p(X) = \ln \sum_{Z}p(X,Z)$$当隐变量是离散变量时,上述公式需要对所有可能的 $Z$ 进行求和,当隐变量维度比较小时,可以计算,但维度非常高时就很难计算;当隐变量为连续变量时,如果假定 $Z$ 为简单的高斯分布,并且条件分布 $p(X|Z)$ 也满足一定条件(比如共轭分布)时,可以计算,但是绝大多数情况下,上述的积分操作是不可计算的。
所以为了优化最大似然,引入下面的 ELBO:
$$ \begin{aligned} \ln p(X) &= \ln \sum_{Z}p(X,Z) \\ &= \ln \Bigg(\sum_{Z}q(Z) \frac{p(X,Z)}{q(Z)} \Bigg) \\ & \geq \sum_{Z} q(Z) \ln \frac{p(X,Z)}{q(Z)} \\ &= \sum_{Z}q(Z) \ln p(X|Z) + \sum_{Z}q(Z) \ln \frac{p(Z)}{q(Z)} \end{aligned} $$上述公式的不等号支出根据 Jensen 不等式得到,最后得到 ELBO 下界:
$$\ln p(X) \geq \sum_{Z}q(Z)\ln p(X|Z) +\sum_{Z}q(Z) \ln \frac{p(Z)}{q(Z)}$$上式不等式右边就是 ELBO,最大化对数似然就变成了最大化 ELBO。ELBO 中的 $q(Z)$ 是对隐变量 $Z$ 引入的变分分布,用来近似真实的隐变量分布 $p(Z)$。所以 ELBO 由两项组成,第一项是给定隐变量时的条件分布的似然,第二项是变分分布和真实分布之间的 KL 距离。
下面是 KL 距离的定义:

在 Mean-Field 变分推断中假设 $q(Z) = \prod _{i=1}^{n}q_i(Z_i)$,即假设 $Z$ 由 $Z_1,Z_2,\cdots,Z_n$ 组成,并满足独立条件。由此可以简化计算,从而得到 $q_i(Z_i)$。一般来说,Mean-Field 得到的结果类似于下面的形式
也就是,$Z_j$ 的分布是由其余所有 $ \{Z_i \}_{i \neq j} $ 对联合分布的对数似然积分得到的,通常也是难以计算的。
总结¶
- 本质上存在着两个encoder,一个计算均值,一个计算方差。
- 它本质上就是在我们常规的自编码器的基础上,对encoder的结果(在VAE中对应着计算均值的网络)加上了“高斯噪声”,使得结果decoder能够对噪声有鲁棒性;而那个额外的KL loss(目的是让均值为0,方差为1),事实上就是相当于对encoder的一个正则项,希望encoder出来的东西均有零均值。
- 而另外一个encoder(对应计算方差的网络)是用来动态调节噪声的强度的。当decoder还没有训练好时(重构误差远大于KL loss),就会适当降低噪声(KL loss增加),使得拟合起来容易一些(重构误差开始下降);反之,如果decoder训练得还不错时(重构误差小于KL loss),这时候噪声就会增加(KL loss减少),使得拟合更加困难了(重构误差又开始增加),这时候decoder就要想办法提高它的生成能力了。
- 重构的过程是希望没噪声的,而KL loss则希望有高斯噪声的,两者是对立的。所以,VAE跟GAN一样,内部其实是包含了一个对抗的过程,只不过它们两者是混合起来,共同进化的。
TensorFlow 简单实现¶

1. 安装&调包
!pip install -q tensorflow-probability
# to generate gifs
!pip install -q imageio
!pip install -q git+https://github.com/tensorflow/docs
from IPython import display
import glob
import imageio
import matplotlib.pyplot as plt
import numpy as np
import PIL
import tensorflow as tf
import tensorflow_probability as tfp
import time
2. 载入数据(MINST)¶

我们使用 MINST 数据来训练变分自编码器,VAE 是 AE 的一个延伸,使得隐变量不在受制于原图而固定,而变成服从于正态分布的均值和标准差的隐变量,形成了一个连续的隐空间,从而增强模型的生成能力。
# 载入
(train_images, _), (test_images, _) = tf.keras.datasets.mnist.load_data()
每个 MINST 图像原本是一个 784 个整数形成的向量,其中每个数字是在 0 - 255 之间的,表示像素的亮度。那么我们要手工对其进行二分化形成一个伯努利分布。
# 图像处理
def preprocess_images(images):
images = images.reshape((images.shape[0], 28, 28, 1)) / 255.
return np.where(images > .5, 1.0, 0.0).astype('float32')
train_images = preprocess_images(train_images)
test_images = preprocess_images(test_images)
train_size = 60000
batch_size = 32
test_size = 10000
3. 批量化 & 打乱
train_dataset = (tf.data.Dataset.from_tensor_slices(train_images)
.shuffle(train_size).batch(batch_size))
test_dataset = (tf.data.Dataset.from_tensor_slices(test_images)
.shuffle(test_size).batch(batch_size))
4. 构建编码 & 解码器
在此,我们使用两个小的卷积层来构建编码和解码器。这些网络实际上也被看作是识别层和生成层。我们使用 tf.keras.Sequential 来构建网络,令 $x$ 和 $z$ 表示观测数据和隐变量。
编码层(Encoder network)¶
这里定义了一个近似后验概率 $q(z|x)$,也就是把观测数据作为输入,然后输出一系列的参数来表达隐变量 $z$ 的条件概率分布。这里,我们把模型简化成高斯分布(算是假设),并且网络输出的是高斯分布的均值和对数方差(加强数值稳定性)。
解码器(Decoder network)¶
解码器定义了观测数据的关于隐变量的条件概率分布 $p(x|z)$,我们要对隐变量先验概率 $p(z)$ 建模。
重参数化技巧(Reparameterization trick)¶
也就是之前提到的
$$z = \mu + \sigma \odot \epsilon$$这样一来就可以解决反向传播不能在随机节点生效的问题,并且把随机性转移到了 $\epsilon$ 上,所以隐变量现在由一个关于 $\mu$、$\sigma$ 还有 $\epsilon$ 的方程,从而使得模型在梯度下降也就是关于重构损失函数对两个参数 $\mu$ 和 $\sigma$ 求导的时候可以反向传播,同时也保证了 $\epsilon$ 的随机性。
网络结构(Network architecture)¶
对于编码层,我们用两个卷积层接着一个全连接层。在解码层中,我们通过使用全连接层,后接三个卷积转置层(在某些情况下也称为反卷积层)来镜像此体系结构。
请注意,在训练 VAE 时避免使用批归一化(batch normalization)是一种常见的做法,因为使用小批量处理会导致额外的随机性,从而加剧随机抽样的不稳定性。
这里,不妨简单介绍一下有关于卷积神经网络的知识:

卷积神经网络(Convolutional Neural Network, CNN)由于其在计算机视觉上的出色表现而出名,其基本结构就是上图的卷积层(Conv)和全连接层(dense)
卷积层进行的处理就是卷积运算。卷积运算相当于图像处理中的“滤波器运算”,对于输入数据,卷积运算以一定间隔滑动滤波器的窗口并应用。
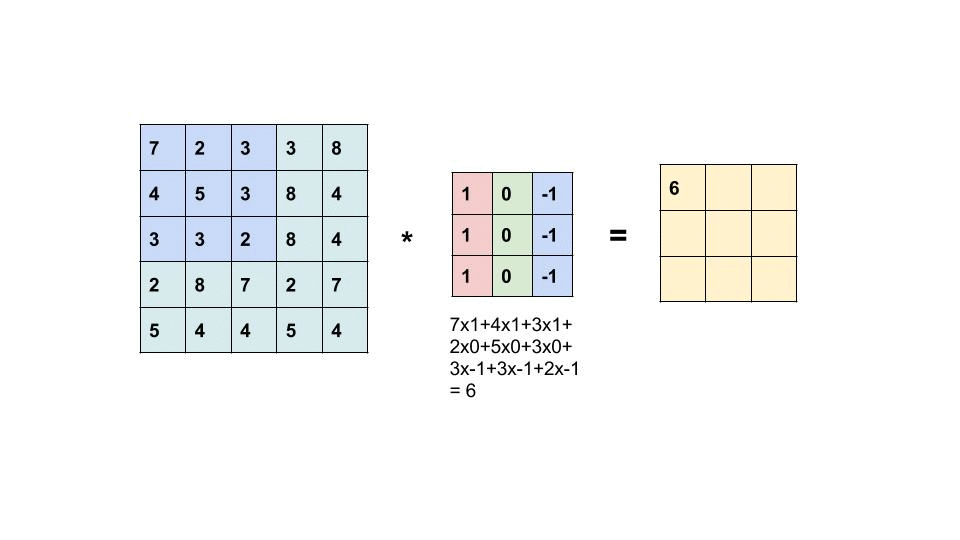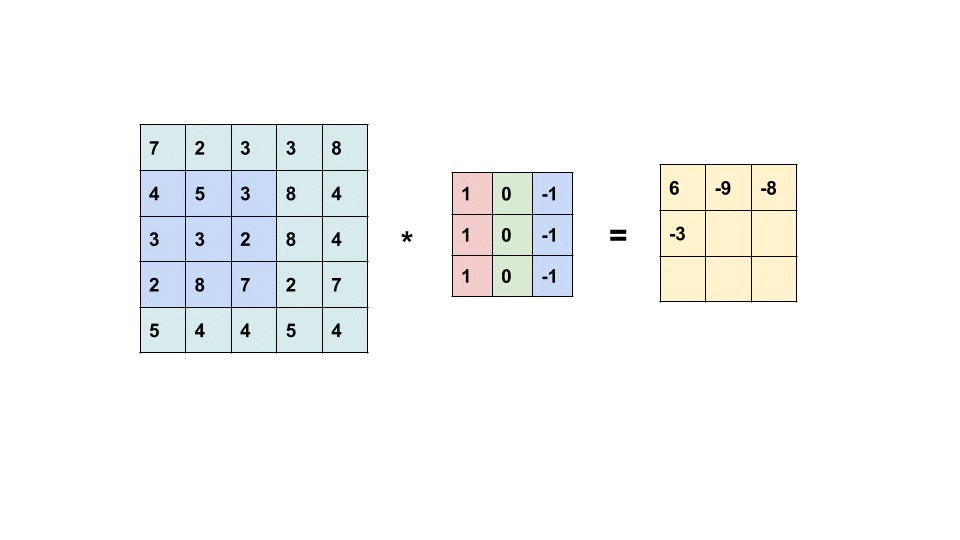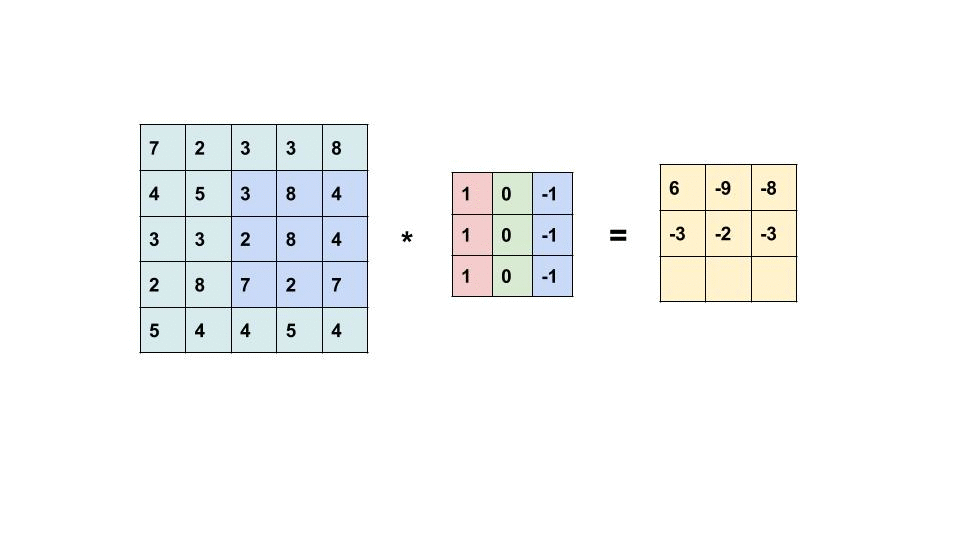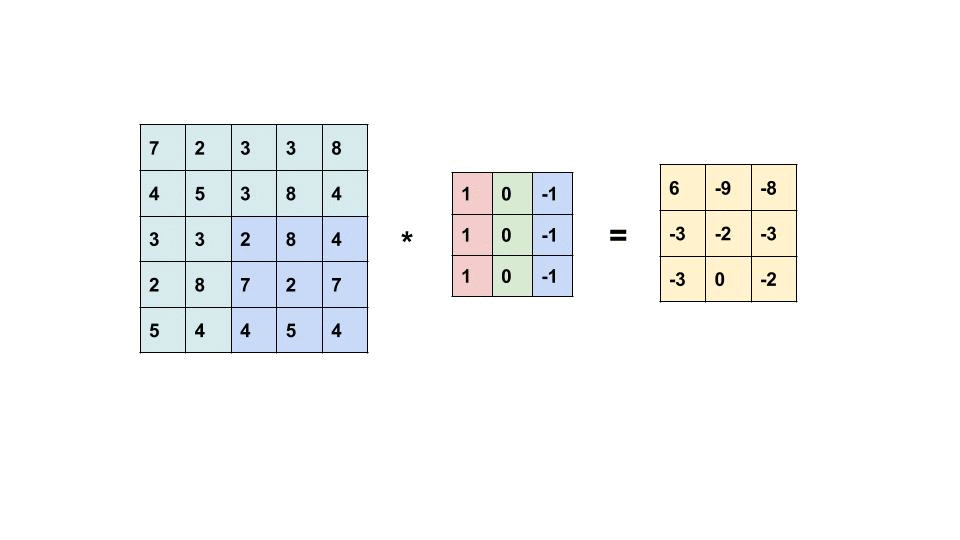
不同的 filter 在卷积层中用来提取源像素中的不同特征并降维,滤波器的每个元素都代表着权重,并且由反向传播来更新。所以实际上编码层的作用就是来降低维度和提取特征,和卷积层的作用十分类似,那么这里不对 CNN 进行展开了,只是加深对 Conv VAE 结构的印象和理解。
5. 卷积 VAE 建模¶
class CVAE(tf.keras.Model):
"""Convolutional variational autoencoder."""
def __init__(self, latent_dim):
super(CVAE, self).__init__()
self.latent_dim = latent_dim
# 编码层
#### 函数解释 ####
"""
1. tf.keras.layers.InputLayer: 输入层
需要给定 input_shape,只指出后三维即可,第一维度按batch_size自动指定
2. tf.keras.layers.Conv2D: 2D 卷积层
参数:
1. filters: 输出空间的维度,也就是我们要压缩到的维度
2. kernel_size: n x n 的filter kernel 大小(也可以自己定义长和宽)
3. strides: 横纵向步长
4. padding: 补0策略,扩充图片, 在图片外围补充一些像素点,把这些像素点初始化为0。为“valid”, “same”。
“valid”代表只进行有效的卷积,即对边界数据不处理。
“same”代表保留边界处的卷积结果,通常会导致输出shape与输入shape相同。
5. activation: 激活函数,不指定则用线性激活函数
3. tf.keras.layers.Flatten: Flatten层用来将输入“压平”,即把多维的输入一维化,
常用在从卷积层到全连接层的过渡。Flatten不影响batch的大小。
4. tf.keras.layers.Dense: 全连接层,起到将学到的“分布式特征表示”映射到样本标记空间的作用。
"""
self.encoder = tf.keras.Sequential(
[
tf.keras.layers.InputLayer(input_shape=(28, 28, 1)),
tf.keras.layers.Conv2D(
filters=32, kernel_size=3, strides=(2, 2), activation='relu'),
tf.keras.layers.Conv2D(
filters=64, kernel_size=3, strides=(2, 2), activation='relu'),
tf.keras.layers.Flatten(),
# No activation
tf.keras.layers.Dense(latent_dim + latent_dim),
]
)
self.decoder = tf.keras.Sequential(
[
tf.keras.layers.InputLayer(input_shape=(latent_dim,)),
tf.keras.layers.Dense(units=7*7*32, activation=tf.nn.relu),
tf.keras.layers.Reshape(target_shape=(7, 7, 32)),
tf.keras.layers.Conv2DTranspose(
filters=64, kernel_size=3, strides=2, padding='same',
activation='relu'),
tf.keras.layers.Conv2DTranspose(
filters=32, kernel_size=3, strides=2, padding='same',
activation='relu'),
# No activation
tf.keras.layers.Conv2DTranspose(
filters=1, kernel_size=3, strides=1, padding='same'),
]
)
@tf.function
def sample(self, eps=None):
if eps is None:
eps = tf.random.normal(shape=(100, self.latent_dim))
return self.decode(eps, apply_sigmoid=True)
def encode(self, x):
mean, logvar = tf.split(self.encoder(x), num_or_size_splits=2, axis=1)
return mean, logvar
def reparameterize(self, mean, logvar):
eps = tf.random.normal(shape=mean.shape)
return eps * tf.exp(logvar * .5) + mean
def decode(self, z, apply_sigmoid=False):
logits = self.decoder(z)
if apply_sigmoid:
probs = tf.sigmoid(logits)
return probs
return logits
6. 定义损失函数 & 最优化函数
VAE 通过在边际对数似然上最大化 ELBO 来进行训练。
之前提到过 KL 散度(Kullback-Leibler Divergence),其衡量的是两个分布之间的相近性,也叫做相对熵,其定义为:
$$ KL(q||p) = E_q \Big[ \log \frac{q(Z)}{p(Z|x)} \Big] $$那么其实我们不能直接对上面的式子最小化,但是我们能对在一定限制下和它类似的方程进行最小化,也就是 ELBO(evidence lower bound),即证据下界。这里的证据指数据或可观测变量的概率密度。
$$\log p(x) \ge \text{ELBO} = \mathbb{E}_{q(z|x)}\left[\log \frac{p(x, z)}{q(z|x)}\right].$$实际当中,我们这个期望的蒙特卡洛估计来最优化:
$$\log p(x| z) + \log p(z) - \log q(z|x),$$其中 $z$ 抽样于 $q(z|x)$.
optimizer = tf.keras.optimizers.Adam(1e-4)
def log_normal_pdf(sample, mean, logvar, raxis=1):
log2pi = tf.math.log(2. * np.pi)
return tf.reduce_sum(
-.5 * ((sample - mean) ** 2. * tf.exp(-logvar) + logvar + log2pi),
axis=raxis)
def compute_loss(model, x):
mean, logvar = model.encode(x)
z = model.reparameterize(mean, logvar)
x_logit = model.decode(z)
cross_ent = tf.nn.sigmoid_cross_entropy_with_logits(logits=x_logit, labels=x)
logpx_z = -tf.reduce_sum(cross_ent, axis=[1, 2, 3])
logpz = log_normal_pdf(z, 0., 0.)
logqz_x = log_normal_pdf(z, mean, logvar)
return -tf.reduce_mean(logpx_z + logpz - logqz_x)
@tf.function
def train_step(model, x, optimizer):
"""Executes one training step and returns the loss.
This function computes the loss and gradients, and uses the latter to
update the model's parameters.
"""
with tf.GradientTape() as tape:
loss = compute_loss(model, x)
gradients = tape.gradient(loss, model.trainable_variables)
optimizer.apply_gradients(zip(gradients, model.trainable_variables))
7. 训练(Training)¶
- 先遍历整个数据集
- 每次迭代过程中,我们把图片丢进编码层得到来估计后验概率 $q(z|x)$ 的参数 $\mu$ 和 $\sigma$
- 接下来,我们用重参数化技巧来从 $q(z|x)$ 里抽样
最后,我们把这些样本传到解码层中来得到生成数据的分布 $p(x|z)$
注意: 由于我们的训练集有6万多条,测试集有1万多条,所导致测试集的 ELBO 会稍微地高一些。
8. 生成图片(Generating images)¶
- 训练完成后,我们可以生成图片
- 先通过从高斯分布 $p(z)$ 来抽取一些隐变量
- 解码层会接着把这些抽出来的 $z$ 编程观测数据的逻辑,给出 $p(x|z)$
- 下面画出伯努利分布的概率
epochs = 10
# set the dimensionality of the latent space to a plane for visualization later
latent_dim = 2
num_examples_to_generate = 16
# keeping the random vector constant for generation (prediction) so
# it will be easier to see the improvement.
random_vector_for_generation = tf.random.normal(
shape=[num_examples_to_generate, latent_dim])
model = CVAE(latent_dim)
def generate_and_save_images(model, epoch, test_sample):
mean, logvar = model.encode(test_sample)
z = model.reparameterize(mean, logvar)
predictions = model.sample(z)
fig = plt.figure(figsize=(4, 4))
for i in range(predictions.shape[0]):
plt.subplot(4, 4, i + 1)
plt.imshow(predictions[i, :, :, 0], cmap='gray')
plt.axis('off')
# tight_layout minimizes the overlap between 2 sub-plots
plt.savefig('image_at_epoch_{:04d}.png'.format(epoch))
plt.show()
# Pick a sample of the test set for generating output images
assert batch_size >= num_examples_to_generate
for test_batch in test_dataset.take(1):
test_sample = test_batch[0:num_examples_to_generate, :, :, :]
generate_and_save_images(model, 0, test_sample)
for epoch in range(1, epochs + 1):
start_time = time.time()
for train_x in train_dataset:
train_step(model, train_x, optimizer)
end_time = time.time()
loss = tf.keras.metrics.Mean()
for test_x in test_dataset:
loss(compute_loss(model, test_x))
elbo = -loss.result()
display.clear_output(wait=False)
print('Epoch: {}, Test set ELBO: {}, time elapse for current epoch: {}'
.format(epoch, elbo, end_time - start_time))
generate_and_save_images(model, epoch, test_sample)
def display_image(epoch_no):
return PIL.Image.open('image_at_epoch_{:04d}.png'.format(epoch_no))
plt.imshow(display_image(epoch))
plt.axis('off') # Display images
9. 展示已保存的图片动图
anim_file = 'cvae.gif'
with imageio.get_writer(anim_file, mode='I') as writer:
filenames = glob.glob('image*.png')
filenames = sorted(filenames)
for filename in filenames:
image = imageio.imread(filename)
writer.append_data(image)
image = imageio.imread(filename)
writer.append_data(image)
import tensorflow_docs.vis.embed as embed
embed.embed_file(anim_file)
10. 展示隐空间的二维流形¶
流形(manifold)是几何中的一个概念,它是高维空间中的几何结构,即空间中的点构成的集合。可以简单的将流形理解成二维空间的曲线,三维空间的曲面在更高维空间的推广。
作用:
- 数据非线性降维
- 刻画数据的本质
可以举个例子。比如三维空间的球体是一个二维流形嵌入在三维空间(2D manifold embedded in 3D space)。之所以说他是一个二维流形,是因为球上的任意一个点只需要用一个二维的经纬度来表达就可以了。
在深度学习领域,最原初的切入点是所谓的Manifold Hypothesis(流形假设)。流形假设是指“自然的原始数据是低维的流形嵌入于(embedded in)原始数据所在的高维空间”。那么,深度学习的任务就是把高维原始数据(图像)映射到低维流形,使得高维的原始数据被映射到低维流形之后变得可分

如果按照现在深度学习界通用的理解(其实是偏离了原意的),二维流形和 Embedding 差不多,就是从原始数据提取出来的特征,也就是那个通过神经网络映射之后的低维向量。
我们这里用 TensorFlow Probability 来给隐空间生成一个标准正态分布。
def plot_latent_images(model, n, digit_size=28):
"""Plots n x n digit images decoded from the latent space."""
norm = tfp.distributions.Normal(0, 1)
grid_x = norm.quantile(np.linspace(0.05, 0.95, n))
grid_y = norm.quantile(np.linspace(0.05, 0.95, n))
image_width = digit_size*n
image_height = image_width
image = np.zeros((image_height, image_width))
for i, yi in enumerate(grid_x):
for j, xi in enumerate(grid_y):
z = np.array([[xi, yi]])
x_decoded = model.sample(z)
digit = tf.reshape(x_decoded[0], (digit_size, digit_size))
image[i * digit_size: (i + 1) * digit_size,
j * digit_size: (j + 1) * digit_size] = digit.numpy()
plt.figure(figsize=(10, 10))
plt.imshow(image, cmap='Greys_r')
plt.axis('Off')
plt.show()
plot_latent_images(model, 20)
