第五章 分数阶差分特征(上)
这一节分为上下两个部分,内容较多,喜欢看的仔细阅读一下,干货!
这一篇看完你会知道:
- 机器学习在金融领域为啥 fail
- 什么是金融数据的Stationarity并如何判断
1. Motivation
由于套利对于市场的强大推进,金融序列展现出了异常低的信噪比,那么什么是信噪比呢?
这还是要回归到机器学习到底能不能在金融领域有效应用的问题(当然,整本书都在讨论这个问题!)
为什么机器学习在很多领域,比如图像识别、语音识别、自然语言处理等等方面,机器学习或者深度学习算法都能有很好的效果,但是这么多年了,机器学习在金融领域的有效应用还没有完全挖掘出来。
机器学习在很多领域似乎很强大,可以识别猫狗、驾驶汽车,甚至在大赛上完虐人类玩家,那么在选股等金融方面的任务中,似乎也应大展拳脚才对啊!但这并没有得到研究的支持,至少现在无。。。。
到底有何不同?
Small Data
资产管理的一个核心问题,回报预测,就是典型的一个小数据问题,都说金融大数据,比如 tick 数据几个 T,bar 也能达到几个 G(不明白tick/bar的看前面的文章),但是这跟工业界数据没法比,况且,就从一个简单的回归问题的公式来看:
左边假设就是要预测的回报,右边就是参数加变量的组合,对于金融数据,我们不是最在乎 N 的大小,而往往更在乎有效的 t 的数量,也就是 T 一定要大一些,数据应该又肥又长才行。不然模型复杂度一上去,样本外测试会让你亏得妈都不认识。
Low Signal-to-noise ratio(低信噪比)
信噪比,它总结了系统中存在多少是可以预测的,那么就以识别猫狗为例,用个不要太复杂的 ResNet 训练个 10 个 epoch 成功率基本达到了 100%,高成功率就意味着这是个高信噪比环境。信号(猫的图像)控制着照片中的噪声源(模糊程度和背景等)。机器学习在这方面就很牛逼。
但对于回报预测,信噪比就不能说是弱了,是弱的一批,这就说名这个一系统本身就充满着随机不确定性,那么具体为啥?
金融市场嘈杂,哪怕最好的投资组合,在一个月甚至一天的波动也许会因为意想不到的信息而疯狂波动。
还有就是我们本身就预测金融市场的信噪比就很低,并一直保持在较低的水平上,随着某些交易者掌握了一些可靠的预测未来价格上涨信息,他们定会交易,知道这种信息不断被市场消磨,把价格推上去,使得价格达到信息所预测的水平,那么其他投资者只被留下极小的可预测性,所以预测性已被定价了,唯一能推动市场的是未预料到的消息或冲击。
还是回到回报预测(return prediction)这个问题,回报的计算方式就有待考究,传统的收益率计算:
整数阶差分移除了信号(return)的记忆性(memory),价格序列有记忆性,因为每个值都依赖于之前很长的历史序列。然而,整数阶差分会抹掉记忆,在一个有限的window不断沿着时间轴往下过滤,之前的信息就被遗忘了,所以我们要在数据转换上下点功夫,因为我们不想舍弃整数阶差分的稳定性特征(stationary transformation),但又不想丢失太多之前的记忆(memory)。
So, we are trapped in the stationary vs. memory dilemma.
2. Stationarity
简单来说,stationarity 就是随着时间推移,序列的均值方差不随时间改变的性质。所以对于研究者来说,他们希望序列能有个稳定的变化,那么这种变化能够通过历史数据以及模型来去学习所谓的 alpha,并且他们认为这种变化能够随着时间一直研究下去,从而挣钱。But, that is a wishful assumption to expect they will persist over time!
但是 alpha 会反噬!alpha约牛逼,越有可能被其他人copy,所以世上便不存在alpha了,因此,每个预测的变化趋势或者说是 pattern 都是短暂的。
还是回到 stationary 这里来,这个性质对于经济学家来说相当重要,所以过去几十年来,似乎在进行建模之前,都先要把数据做一些平稳性处理。
但是单单从一个有限的样本路径来看,是不可能检验序列是否平稳的!

单看上面这个图,很明显不满足 stationary 的情况,因为序列的均值方差都随着时间在变化,可以用 ADF test 去检验一下。
得到:
1ADF Statistic: 4.2641552p-Value: 1.0000003Critical Values:41%: -3.437055%: -2.8645610%: -2.5683
ADF 检验 p 值过大,明显不能拒绝原假设,也就是说明序列是不平稳的。
但是,如果我现在告诉你上面的图是来自于一个高斯分布(mean 为 100)且自协方差方程满足:
那么肯定认为这一定是个平稳性序列,因为均值和自协方差都是不随时间变化的。

这是把时间维度扩大所得图像。
再用 ADF test 检验一下得到:
xxxxxxxxxx61ADF Statistic: -4.27022p-Value: 0.00053Critical Values:41%: -3.444055%: -2.8676610%: -2.5700
很明显拒绝了原假设,所以说明序列是平稳的,并且置信度很高,p值达到了 0.05%。
可以看出,第一个图中包含了足够多的样本数量,也就是样本容量虽然够大,但是时间跨度却不够,也间接说明金融数据的 small data 问题,所以很明显,没有其他的假设的情况下,不可能从一个有限的时间跨度来判定序列是否稳定。
第五章 分数阶差分特征(中)
这一篇看完你会知道:
- 什么是平稳性(stationary)和差分(differencing)
- 分数阶差分的方法具体是什么(emmm理论推导)
1. Stationary & Differencing
说到整数差分,或者与 differentiation 相关的,你肯定首先想到时间序列里面学到的 ARIMA,那么为啥要差分之前那篇文章说的很清楚了,就是要让序列变得 Stationarity,但是过度的差分又会使模型丢失 memory,从而丧失一大部分预测能力,所以我们才想办法看看能不能做一个权衡,搞个分数差分出来。
ok, just a little review.
不过,那么一个序列是完全平稳的话,就完全没有预测的必要了,因为模型的参数不会随着时间改变,现在是啥以后还是啥,那还预测个啥,图像来说就基本是平的。
那么,你是否有信心能够分辨出下面这几个图哪些是 stationary 的呢?

季节性(seasonality)排除了系列 (d)、(h) 和 (i)。趋势性(trend)排除了系列 (a)、(c)、(e)、(f) 和 (i),只剩下 (b) 和 (g) 是平稳序列。
可以发现,(b)就是(a)的差分,从而序列变得平稳了,那么差分就是连续观测值的差值,就这么简单。
Differencing can help stabilise the mean of a time series by removing changes in the level of a time series, and therefore eliminating (or reducing) trend and seasonality.

学过 R 的朋友,应该知道 ACF 那个图哈,就是 auto-correlation function,它是关于不同的延滞值而画出的序列自相关系数,自相关就是自己跟自己的相关系数,那有人说了,那不等于1么?是的,但是在时间序列中,不同时间下的同一序列的自相关系数是不一样的,这里不再展开了。
2. Backshift Operator
那么既然了解了差分的基本原理和基础,我们来说一下 backshift operator,可以叫做延滞算子?我也不清楚,我们就命名为 吧,这个 ,它满足对于任意的自然数 ,,其中 是特征所形成的向量。
举个例子,,其中 ,所以
根据二项式展开公式,我们有
那么,对于一个实数 ,我们有
同理可推导
3. Weighting Estimation
我们经过展开之后,特征向量 的权重可以用 来表示
其中这个权重 就是上面含 的单项式的系数
并且 为

可以看到 (1) 中,如果 d 是一个正整数,那么第三项之后就全变成 0 了,因此隐藏在第三项之后的memory就被清除了。
可以发现,随着 的增大, 的变化是由规律的
可以发现,
- 当 为 0 时(最上面那条线),只有 ,其他都是 0。
- 当 为 1 时(最下面那条线),,其他都是 0。
- 剩下当 为 0 到 1 之间的分数时,所有曲线都夹在他们中间,并且,都不为 0, 但是随着 的不断增大, 都从一个负数逐渐趋于0。
那么再来看一下 的情况:

变得有一些不一样了是吧,但是这些曲线随着 的增加,最后都收敛到 0 了!
下面是上面曲线的代码,有兴趣可以看一下,有详细的备注!
x1import matplotlib.pyplot as plt2import pandas as pd34# 计算权重 omega5def getWeights(d,size):6# thres>0 drops insignificant weights7 w=[1.]8 for k in range(1,size):9 w_=-w[-1]/k*(d-k+1)10 w.append(w_)11 w=np.array(w[::-1]).reshape(-1,1)12 # 倒序排序并且reshape成一列13 return w1415# 画图16def plotWeights(dRange,nPlots,size):17 # 思路:18 # 对每个d求其对应size的weight19 # 然后根据index来outer join到一起20 w=pd.DataFrame()21 for d in np.linspace(dRange[0],dRange[1],nPlots):22 d = round(d,1)23 w_=getWeights(d,size=size)24 w_=pd.DataFrame(w_,index=range(w_.shape[0])[::-1],columns=[d])25 w=w.join(w_,how='outer')26 ax=w.plot(figsize = [12,8])27 ax.legend(loc='upper left')28 return2930plotWeights(dRange=[0,1],nPlots=11,size=6)31plotWeights(dRange=[1,2],nPlots=11,size=6)3233# have a try!4. Iterative Convergence
那么,如果 不断增大,之后的曲线还会随着 增大继续收敛么?
没错!
通过这个式子,我们可以发现,通过不断地迭代,当 时,,当然这里的 。从而,权重就会逐渐地趋近 0。


总结起来就是:
那么,这一期就讲到这里,你应该了解下面几点:
- 什么是 stationary 和 differencing
- 什么是 backshift operator
- 理解分数阶差分是如何避免整数阶差分而导致的memory loss
- 学会构造分数阶差分的原理,并且掌握不同的 所带来的不同特征
前两周参加公司合唱比赛,丢了半条命,最近身体欠佳所以更新迟了,不过会继续努力的!BTW,我准备开通一个 video channel!但是还在准备中,重点放在本科数学狗留美攻略,以及中英文的数统知识以及机器学习等方面的对照讲解,emmm,反正还在准备中,到时候请大家多多支持啦!
OK,希望这期内容对大家有帮助,下期再见!
第五章 分数阶差分特征(下)
这一篇看完你会知道:
- 分数阶差分的两个替代方法(Expanding window和FFD)
- 分数阶差分的适用场景以及代码实战!
现在,要介绍两个分数阶差分的替代方法
- 传统的 expanding window 方法
- 新的 fixed-width window fracdiff (FFD)
1. Expanding Window
那么首先来说一下,什么是 Expanding Window 呢?接触过 ARIMA 处理过时间序列的人应该了解 Rolling Window 是什么,那么我们就简单对他们做一下解释并对比他们的不同。
just a window
窗户,大家都很熟悉了,上面这个图就是个普通到不能再普通的窗户了,简而言之,窗户的大小决定了我们能透过窗户看到的视野范围的大小。所以对于数据来说也一样,一个移动的窗户可以帮助我们研究数据的一部分。
(1) Rolling Windows
假设,我们想知道每一天的之前5天的股票平均价格,那么我们应该使用 rolling windows,随着窗口的移动,我们在每次移动过程中都可以计算出窗口数据的均值,最终形成了一条曲线,如下图。
xxxxxxxxxx111plt.figure(figsize = [12,8])2data = [100,101,99,105,102,103,104,101,105,102,99,98,105,109,105,120,115,109,105,108]3#Create pandas DataFrame from list4df = pd.DataFrame(data,columns=['close'])5#Calculate a 5 period simple moving average6sma5 = df['close'].rolling(window=5).mean()7#Plot8plt.plot(df['close'],label='HS300')9plt.plot(sma5,label='SMA',color='red')10plt.legend(prop = {'size':20})11plt.show()
随着 rolling window 不断前进,形成的动图如下:
(2) Expanding Windows
Expanding Windows 则是固定了一个 starting point,然后随着数据的加入,窗口的 size 越来越大。
就像下面这样!
xxxxxxxxxx151plt.figure(figsize = [12,8])2#Random stock prices3data = [100,101,99,105,102,103,104,101,105,102,99,98,105,109,105,120,115,109,105,108]4#Create pandas DataFrame from list5df = pd.DataFrame(data,columns=['close'])6#Calculate expanding window mean7expanding_mean = df.expanding(min_periods=1).mean()8#Calculate full sample mean for reference9full_sample_mean = df['close'].mean()10#Plot11plt.plot(df['close'],label='HS300')12plt.plot(expanding_mean,label='Expanding Mean',color='red')13plt.axhline(full_sample_mean,label='Full Sample Mean',linestyle='--',color='red')14plt.legend(prop = {'size':20})15plt.show()
随着 window size不断增大,形成的动图如下:
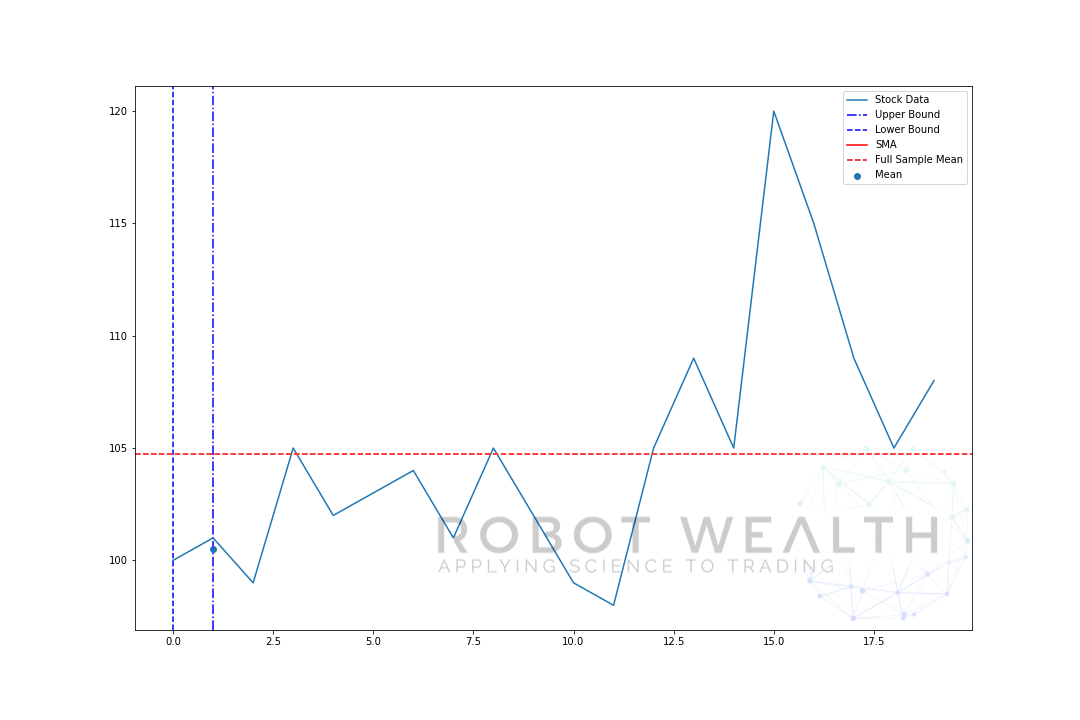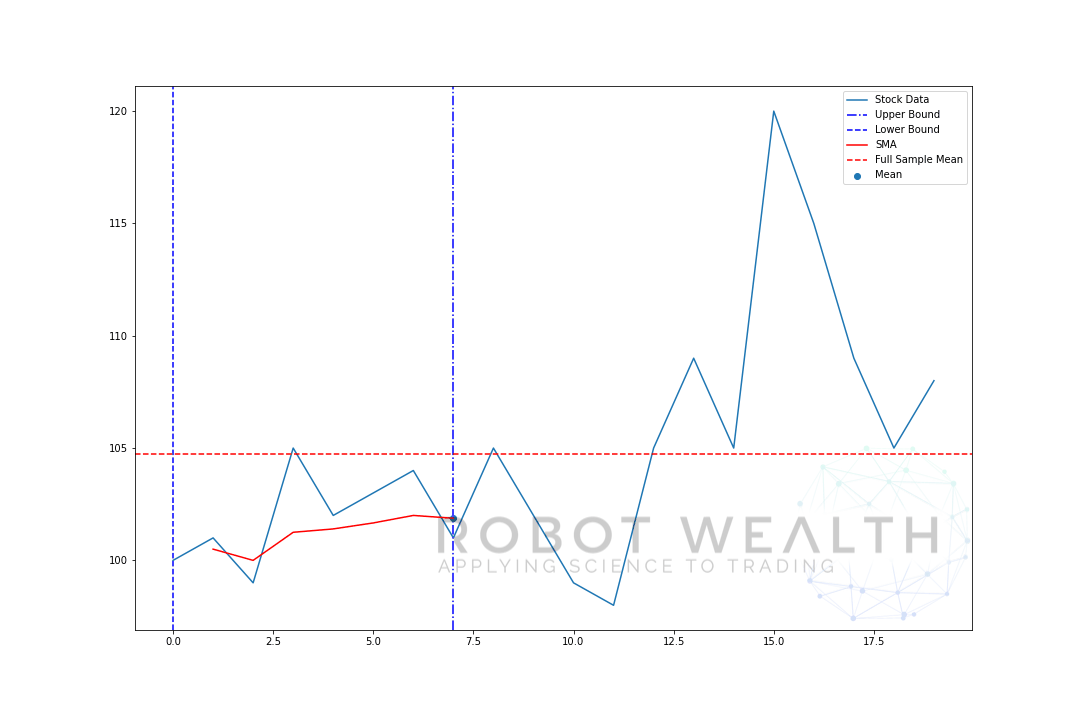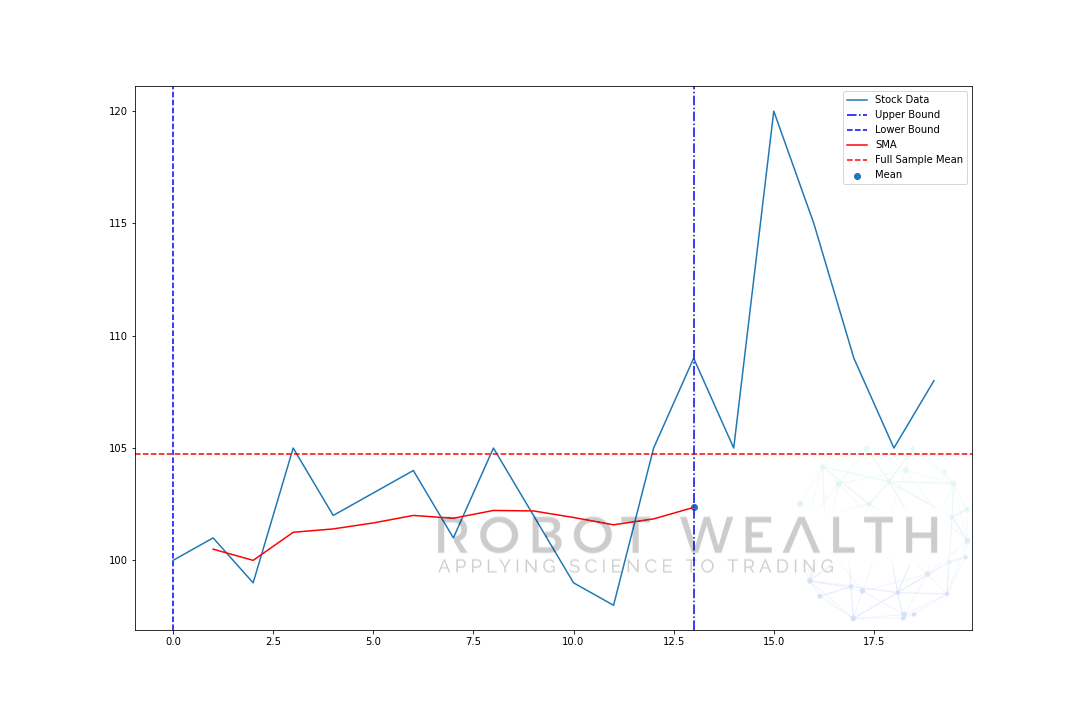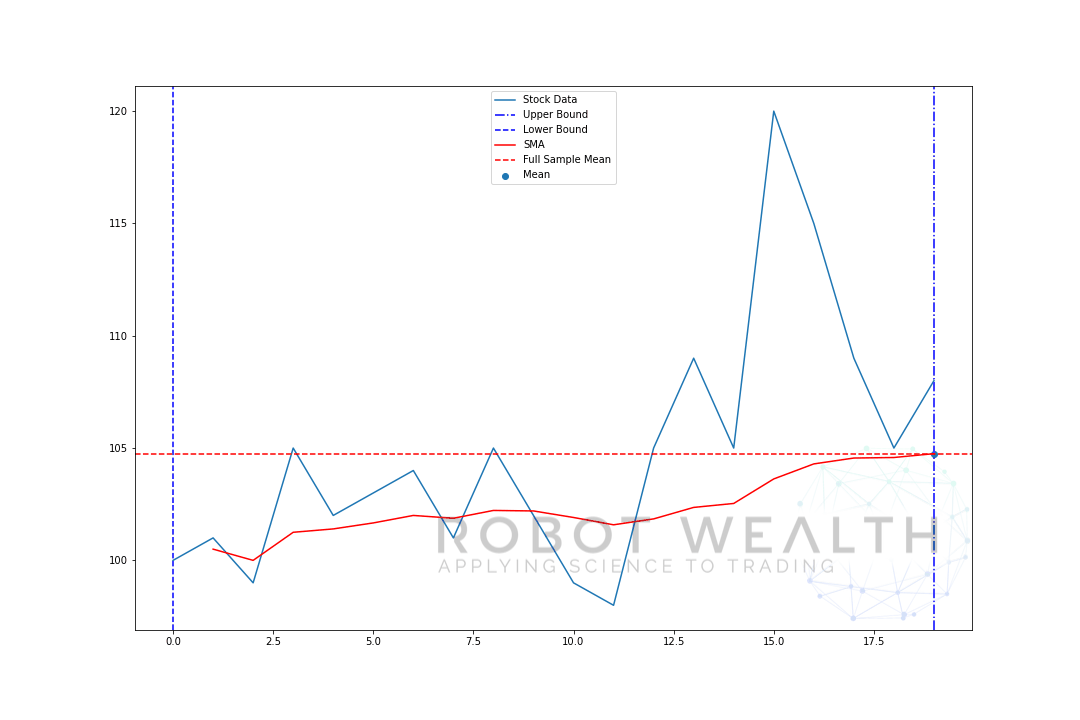
总结一下:
“在这一点,之前的 n 个值的平均值是多少”
用 rolling window
“在这一点,之前所有可获取的数据的平均值是多少”
用 expanding window
下面两个图分别表示沪深300(HS300)的收盘价的分数差分情况,第一个的参数为 ,第二个为 。
可看到当 不变时,确实我们把 tolerance 降低之后,前边的数据被 drop 掉更多了!而且序列也在保持跟蓝色曲线走势的同时,兼顾了平稳性!(代码我放在下面)
681import pandas as pd2import numpy as np3import matplotlib.pyplot as plt4import seaborn as sns5%matplotlib inline67# (1) 定义 fractional differencing function8def fracDiff(series,d,thres=.01):9 '''10 Increasing width window, with treatment of NaNs11 Note 1: For thres=1, nothing is skipped.12 Note 2: d can be any positive fractional, not necessarily bounded [0,1].13 '''14 #1) Compute weights for the longest series15 w=getWeights(d,series.shape[0])16 #2) Determine initial calcs to be skipped based on weight-loss threshold17 w_=np.cumsum(abs(w))18 w_/=w_[-1]19 skip=w_[w_>thres].shape[0]20 #3) Apply weights to values21 df={}22 for name in series.columns:23 seriesF,df_=series[[name]].fillna(method='ffill').dropna(),pd.Series(dtype = 'float64', index = np.arange(series.shape[0]))24 #print(seriesF)25 for iloc in range(skip,seriesF.shape[0]):26 #print(iloc)27 loc=seriesF.index[iloc]28 #print(loc)29 #if not np.isfinite(series.loc[loc,name]):continue # exclude NAs30 #print(np.dot(w[-(iloc+1):,:].T,seriesF.loc[:loc])[0][0])31 df_[loc]=np.dot(w[-(iloc+1):,:].T,seriesF.loc[:loc])[0,0]32 #print(df_)33 df[name]=df_.copy(deep=True)34 df=pd.concat(df,axis=1)35 return df3637# 获取沪深300数据38import tushare as ts39df = ts.get_k_data('hs300',start = '2016-01-01')40raw_df = df[['open','close','high','low']]41new_df = fracDiff(series = raw_df, d = 0.4, thres = 0.01)4243# (2) 画图44def plotExpandingWindow(raw_df,new_df,column = 'close'):45 plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签46 x = np.arange(raw_df.shape[0])47 y1 = raw_df[column]48 y2 = new_df[column]4950 fig = plt.figure(figsize = [40,20])5152 ax1 = fig.add_subplot(111)53 ax1.plot(x, y1,linewidth = 6)54 ax1.set_ylabel(column+" price for HS300 BEFORE expanding window differencing",size = 35, color = 'b')55 ax1.set_title("HS300使用Expanding Window前后对比图"+"",size = 40)56 ax1.set_title("{0} {1}".format("HS300使用Expanding Window前后对比图 ==>", column.upper()),size = 60)57 58 59 ax2 = ax1.twinx() # this is the important function60 ax2.plot(x, y2, '#C70039',alpha=0.6)61 ax2.set_ylabel(column+" price for HS300 AFTER expanding window differencing",size = 35, color = 'r')6263 plt.show()64 return65 66# 画出 open close high low 四种对比图 67for col in raw_df.columns:68 plotExpandingWindow(raw_df,new_df,column = col)2. Fixed-Width Window Fracdiff
那么之前介绍了 Expanding Window 的方法,现在再介绍一个基于 Rolling Window 的方法,也就是固定 window size,同理我们认为如果 落到了一个给定区间,也就是小于一个阈值 。
这种方法的好处在于可以避免 expanding window 所带来的累积驱动效应而导致的 negative drift,也就是由于累积动量产生的定向偏移。
对上面的代码加以改进,我们可以得到:
xxxxxxxxxx601def get_weight_ffd(d, thres, lim = len(series)):2w, k = [1.], 13ctr = 04while True:5w_ = -w[-1] / k * (d - k + 1)6if abs(w_) < thres:7break8w.append(w_)9k += 110ctr += 111if ctr == lim - 1:12break13w = np.array(w[::-1]).reshape(-1, 1)14return w1516def fracDiff_FFD(series,d,thres=1e-5):17'''18Constant width window (new solution)19Note 1: thres determines the cut-off weight for the window20Note 2: d can be any positive fractional, not necessarily bounded [0,1].21'''22#1) Compute weights for the longest series23w=get_weight_ffd(d,thres)24width=len(w)-125#2) Apply weights to values26df={}27for name in series.columns:28seriesF,df_=series[[name]].fillna(method='ffill').dropna(),pd.Series()29for iloc1 in range(width,seriesF.shape[0]):30loc0,loc1=seriesF.index[iloc1-width],seriesF.index[iloc1]31if not np.isfinite(series.loc[loc1,name]):continue # exclude NAs32df_[loc1]=np.dot(w.T,seriesF.loc[loc0:loc1])[0,0]33df[name]=df_.copy(deep=True)34df=pd.concat(df,axis=1)35return df36def plotExpandingWindow_FFD(raw_df,new_df,column = 'close'):38plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签39x = np.arange(raw_df.shape[0])40y1 = raw_df[column]41y2 = new_df[column]4243fig = plt.figure(figsize = [40,20])4445ax1 = fig.add_subplot(111)46ax1.plot(x, y1,linewidth = 6)47ax1.set_ylabel(column+" price for HS300 BEFORE FFD differencing",size = 35, color = 'b')48ax1.set_title("HS300使用FFD前后对比图"+"",size = 40)49ax1.set_title("{0} {1}".format("HS300使用FFD前后对比图 ==>", column.upper()),size = 60)50ax2 = ax1.twinx() # this is the important function53ax2.plot(x, y2, '#C70039',alpha=0.6)54ax2.set_ylabel(column+" price for HS300 AFTER FFD differencing",size = 35, color = 'r')5556plt.show()57return58for col in raw_df.columns:60plotExpandingWindow_FFD(raw_df,new_df,column = col)
可以明显看出来,平稳化后的序列比 Expanding Window 的序列要短一些,但是更加平稳了!**
那么这时候,我们自然想着是否能在最大化去保存 memory 的同时,能否也尽量保证序列的平稳性。
FFD 中的主要影响参数是 ,那么我们可以根据不同的 来测试序列的平稳度,并画出曲线。这个 可以说是我们需要移除多少 memory 才能保证序列的 stationary 的变量,当原始序列是很不平稳的时候,我们初步应该选择 。
上图的右侧 y 轴表示基于 close price 取对数计算的 ADF 统计量,横坐标是 。
所以,实际情况当中,我们可以按照以下 4 步来进行:
计算时间序列的累计和,确认序列的平稳程度,以及是否需要差分
使用不同的 计算
FFD(d)序列,如果序列极其不平稳,那么 应该首选趋于 0 的小数确定一个能使得
FFD(d)的 ADF test 统计量的 p 值低于 5% 的 d(一般小于0.6)使用
FFD(d)序列作为新的预测特征
小结
OK,那么关于第五章的分数阶差分特征的内容就到这里啦,希望对大家关于 “金融序列在保证平稳性的同时能使得记忆最大化” 这一问题上有新的理解,希望大家多多写写代码,试试不同参数,说不定会有意想不到的效果!下期见~

