AFML Sample Weights

本文关于为金融数据采样权重的方法逐一介绍

• 第四章 金融数据采样权重

  • 4.1 动机
  • 4.2 Sample Weights

4.1 MOTIVATION

上一章讲了一些对金融数据打标签的方法，包含依赖路径的TB法，基于次级模型（ML模型）的元标签法，那么都是为了将连续的股价标记成离散的结果，是因为股价的时间自相关性较强，波动性较大。

那么现在要讨论一下如何使用采样权重来处理另一个问题，也就是数据不满足IID，也就是样本之间独立同分布，很多方法在金融领域失败的原因就是基于金融时间序列来说，对于数据的假设是不成立的。

4.2 OVERLAPPING OUTCOMES

我们之前对于一个给定的样本 $X_i$，对其打标签 $y_i$，其中 $y_i$ 是发生在时间区间 $[t_{i,0}, t_{i,1}]$ 的 bar 的函数，这基于我们选用什么打标签的方法。当 $t_{i,1} > t_{j,0}$ 并且 $i<j$，那么 $y_i$ 和 $y_j$ 两个会依赖于一个共同的 return --> $r_{t_{j,0}, \min \{t_{i,1},t_{j,1}\}}$，也就是在时间区间 $[t_{j,0}, \min \{t_{i,1},t_{j,1}\}]$ 里的 return。

解释一下：这里的 “当 $t_{i,1} > t_{j,0}$ 并且 $i<j$” 指的是

第i个样本在第1时刻的时间点 标记为 $t_{i,1}$；第j个样本在第0时刻的时间点 标记为 $t_{j,0}$，并且 $i<j$。

相当于第i个样本对应的打标签时间区间 $[t_{i,0}, t_{i,1}]$ 和 第j个样本对应的打标签时间区间 $[t_{j,0}, t_{j,1}]$ 重叠了，从而 $y_i,y_j$就会取决于其时间区间的交集所对应的的 return。所以在当两个连续的outcome存在overlap的时候，就不能保证 $\{y_i \}_{i=1,\cdots,I}$ 是 IID 的。

那么对于overlap的解释可以进一步用图形来解释

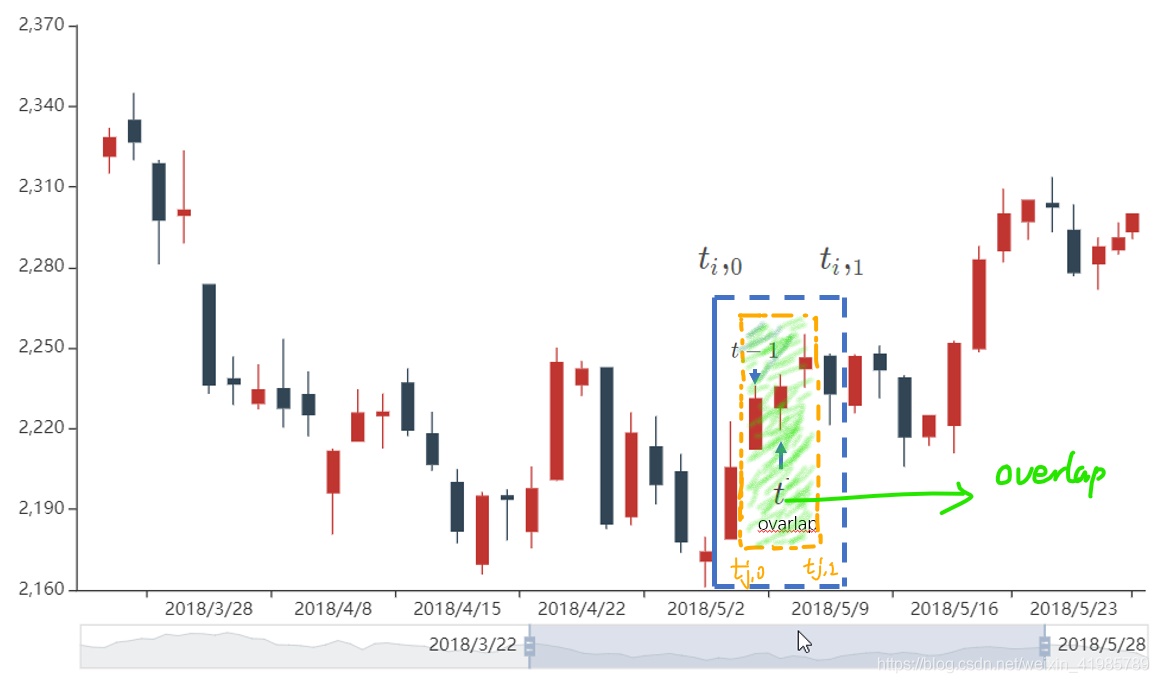
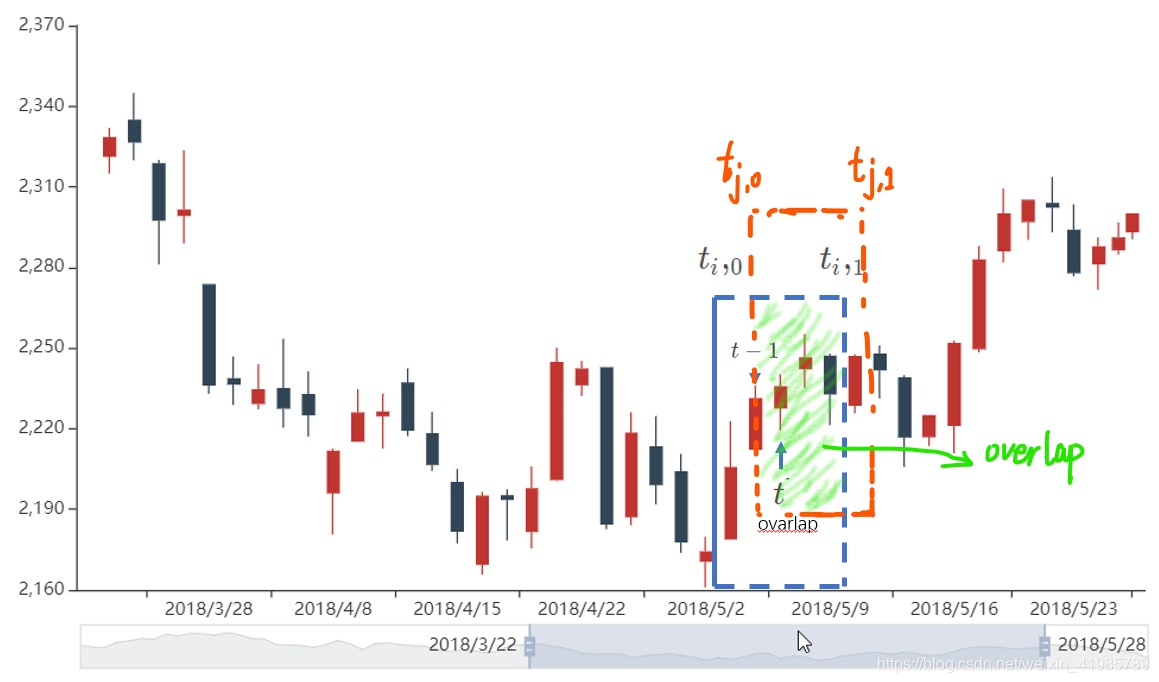
那么如何避免这个问题呢？

强行限制 $t_{i,1}$ 一定小于 $t_{j,0}$

那么这样做，确实不会出现overlap了，因为每个特征的outcome都在下一个时间区间开始或之前就被决定了。但是，这种硬性条件会使得

1. 样本的采样频率受限，就是说采样的时间区间必须和outcome的时间区间一致。
2. 基于路径的标签方法会使得采样频率受限于第一次隔栏接触的时间区间，则设定的时间区间必须要与每一个三隔栏内任意一隔栏触碰到的最小时间区间，不然触及到隔栏之后你还在采样，数据就有错误了。

这种情况可谓是金融应用的一个特点，大部分的非金融 ML 研究者假设样本是 IID 的。例如，我们可以从大量患者那里获得血液样本，并对其进行测量胆固醇。当然，各种潜在的共同因素将改变均值和胆固醇分布的标准差，但样本仍是独立的：每个受试者有一个观察结果。假设采集这些血液样本，并且实验室中的某人从每根试管中不下心倒出血液进入以下九支在他们的右边的管。即，管10含用于患者10的血液，但也包含来自患者1至9的血液。试管11包含患者11的血液，也包含患者2至10的血液，就类似与MA的划框的感觉，所以当去判断高血压等病症使，我们并不确定每个病人的血压水平，因为他们并不独立存在。

那么到底该怎么解决？引入 Sample Weights

4.3 NUMBER OF CONCURRENT LABELS

当标签 $y_i$ 和 $y_j$ 都是至少一个共同的 return，$r_{t-1,t} = \frac{P_t}{P_{t-1}}-1$ 的函数，那么在时点 $t$ 上，他们是同时发生的，相当于根据至少一个共同的 return 来决定的。那么我们要计算是关于一个给定的 return 的 label 数量有多少。

1. 对于每个时间点 $t = 1, \cdots, T$，我们创造一个二元数组，$\{ 1_{t,i}\}_{i=1,\cdots,I}$，其中 $1_{t,i} \in \{0,1\}$。变量 $1_{t,i}=1$ 当且仅当 $[t_{i,0},t_{i,1}]$ 和 $[t-1,t]$ 重叠，否则为 0。
2. 聚合所有的 1，$c_t = \sum_{i=1}^{I}1_{t,i}$也就得到了同时发生的 label 数量。

​x
1
def mpNumCoEvents(closeIdx,t1,molecule):
2
    '''
3
    计算每个 bar 的 同时发生的 label 数量: 
4
        Compute the number of concurrent events per bar.
5
        +molecule[0] is the date of the first event on which the weight will be computed
6
        +molecule[-1] is the date of the last event on which the weight will be computed
7
        Any event that starts before t1[molecule].max() impacts the count.
8
    '''
9
    
10
#1) find events that span the period [molecule[0],molecule[-1]]
11
t1=t1.fillna(closeIdx[-1]) # unclosed events still must impact other weights
12
t1=t1[t1>=molecule[0]] # events that end at or after molecule[0]
13
t1=t1.loc[:t1[molecule].max()] # events that start at or before t1[molecule].max()
14
​
15
#2) count events spanning a bar
16
iloc=closeIdx.searchsorted(np.array([t1.index[0],t1.max()]))
17
count=pd.Series(0,index=closeIdx[iloc[0]:iloc[1]+1])
18
for tIn,tOut in t1.iteritems():count.loc[tIn:tOut]+=1.
19
return count.loc[molecule[0]:t1[molecule].max()]

4.4 AVERAGE UNIQUENESS OF A LABEL

下面，我们将要估计标签的独立度也就是不重叠度。首先，先来定义一下这个变量。

1. 标签 $i$ 在时点 $t$ 的独立度是 $u_{t,i} = 1_{t,i}c_t^{-1}$

2. 标签 $i$ 的平均独立度是

   $$\begin{aligned} \overline u_i &= \frac{\sum_{t=1}^{T}u_{t,i}}{\sum_{t=1}^{T}1_{t,i}} \\ &= \frac{\sum_{t=1}^{T}1_{t,i}c_t^{-1}}{\sum_{t=1}^{T}1_{t,i}} \\ &= \Bigg(\frac{\sum_{t=1}^{T}1_{t,i}}{\sum_{t=1}^{T} \frac{1_{t,i}}{c_t}} \Bigg)^{-1} \end{aligned}$$

那么我们知道调和平均值的公式：

那么我们可以把 $1_{t,i}$ 看作调和平均值公式里的 $w_i$，也就是权重，那么平均独立度就是基于 concurrent 事件发生的期限的调和平均值的倒数，也就是以 concurrent label 为权重的关于样本的调和平均值。

FIGURE 4.1 表示了来自于竖隔栏的独立度（我们以后用 avgU 来表示）的直方图。

计算关于 label i 的 avgU，需要未来才能获取的信息。这会造成overfitting么？要注意 $\{ \overline u_i\}_{i=1,\cdots,I}$ 是被应用在训练集和标签信息所合并的数据里，并不在测试集中，所以测试集依旧是完好无损的，不构成信息泄露。

4.5 BAGGING CLASSIFIERS AND UNIQUENESS

先来看个例子，根据概率统计的基本知识，我们知道从 I 个物体中有放回的抽取一个特定的物体 i，在 I 次抽取中没有取到的概率是：

$I^{-1}$ --> 抽到 i 的概率

$1-I^{-1}$ --> 没有抽到 i 的概率

$(1-I^{-1})^{I}$ --> 总共抽 I 次，都没有抽到 i 的概率

所以，

也就表示任意一个物体没有被抽到的概率约为 $e^{-1} = 0.368$。

那么反之，不重复的物体被抽到的概率为 $1-e^{-1}$。（这里 i 是任意的，也就是任意的 i 被抽到的概率，i 是不重复的）

假设我们有 I 个样本，不重叠样本的最大值是 K。那么在 I 次有放回的抽取后，没有抽到 i 的概率为 $(1-K^{-1})^{I}$ 。随着 I 的增大，这个概率变为 $e^{-\frac{K}{I}}$。也就意味着不重叠样本数的抽取量会更小，因为 $1-e^{-\frac{K}{I}} \leq 1-e^{-1}$。也说明了假设数据是 IID 会造成过采样。

那么在 bootstrap 也就是有放回的抽样的结果下，avgU 远小于 1，这就造成抽样的数据重叠度会很高，这样的抽样貌似没什么意义。

举个例子，在随机森林里，所有的树会由一个单树（overfit）复制过来，或者说他们的相似度很高，随机抽样会造成抽样的结果和未被抽样的数据很相似，那么我们应该如何处理呢？

1. 在 bootstrap 之前 drop 重叠的数据。因为并不是完美重叠，那么drop掉的话会造成信息损失，并不是很好的办法。
2. 使用 avgU 去降低含有冗余信息的数据的影响。这里我们强制所抽取数据的抽样频率小于等于其唯一度。
3. 更好的办法是进行 sequential bootstrap。

Sequential Bootstrap

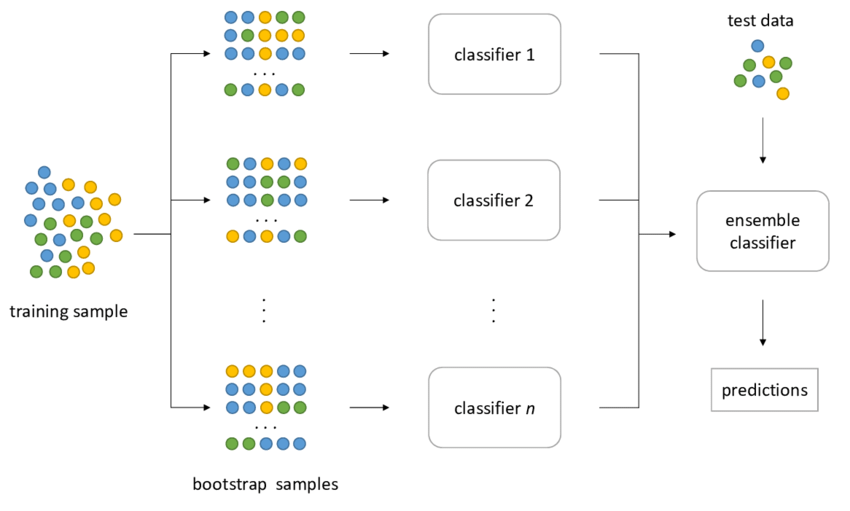
也就是根据一个时时改变的抽样概率来控制重复度。

步骤大概如下：

1. 按照均匀分布抽一个样本 $X_i$，$i \sim U[1,I]$，那么其概率为 $\delta_{i}^{(1)} = I^{-1}$。

2. 第二次抽样，我们希望降低重叠的概率。但是要知道 bootstrap 是可重复抽样的，所以是有可能再抽到一样的数据，那么用 $\varphi$ 来表示自此已经抽到的数据序列，包含重复的抽取。那么到现在，我们只抽了一个样本，那么 $\varphi^{(1)} = \{i\}$。那么关于 j，$j\neq i$，在时点 t 的唯一度为 $u_{t,j}^{(2)} = 1_{t,j}(1+\sum_{k\in\varphi^{(1)}}1_{t,k})^{-1}$，这算是添加 j 到原来的序列之后的唯一度，那么 $\overline u_j^{(2)} = (\sum_{t=1}^{T}u_{t,j})(\sum_{t=1}^{T}1_{t,j})^{-1}$

3. 根据更新的抽样概率来抽取第二个样本。

   $$\delta_j^{(2)} = \overline u_j^{(2)} \Bigg(\sum_{k=1}^{I} \overline u_k^{(2)} \Bigg)^{-1}$$

   概率最后被归一化

实例：

考虑到我们有3个标签，$\{ y_i\}_{i=1,2,3}$，其中

• $y_1$ 是 $r_{0,3}$ 的方程
• $y_2$ 是 $r_{2,4}$ 的方程
• $y_3$ 是 $r_{4,6}$ 的方程

那么我们可以构造一个 indicator matrix，也就是 $\{1_{t,j} \}$，其中 t 代表return所基于的时间，j 代表第 j 个样本。

1. 按照均匀分布随机抽样，$\delta_i = 1/3$，假设我们抽到了2

2. 那么

   第一个feature的uniqueness为

   $$\overline u_1^{(2)} = (1+1+1/2)/3 = 5/6<1$$

   第二个feature的uniqueness为

   $$\overline u_2^{(2)} = (1/2+1)/2 = 3/4<1$$

   第三个feature的uniqueness为

   $$\overline u_3^{(2)} = (1+1)/2 = 1$$

   代码结果：

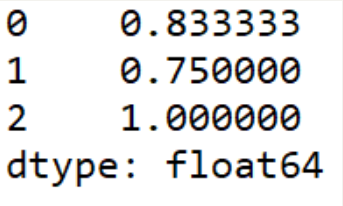
3. 计算第二次抽样的概率，也就是上面的每个数除以他们的和

代码

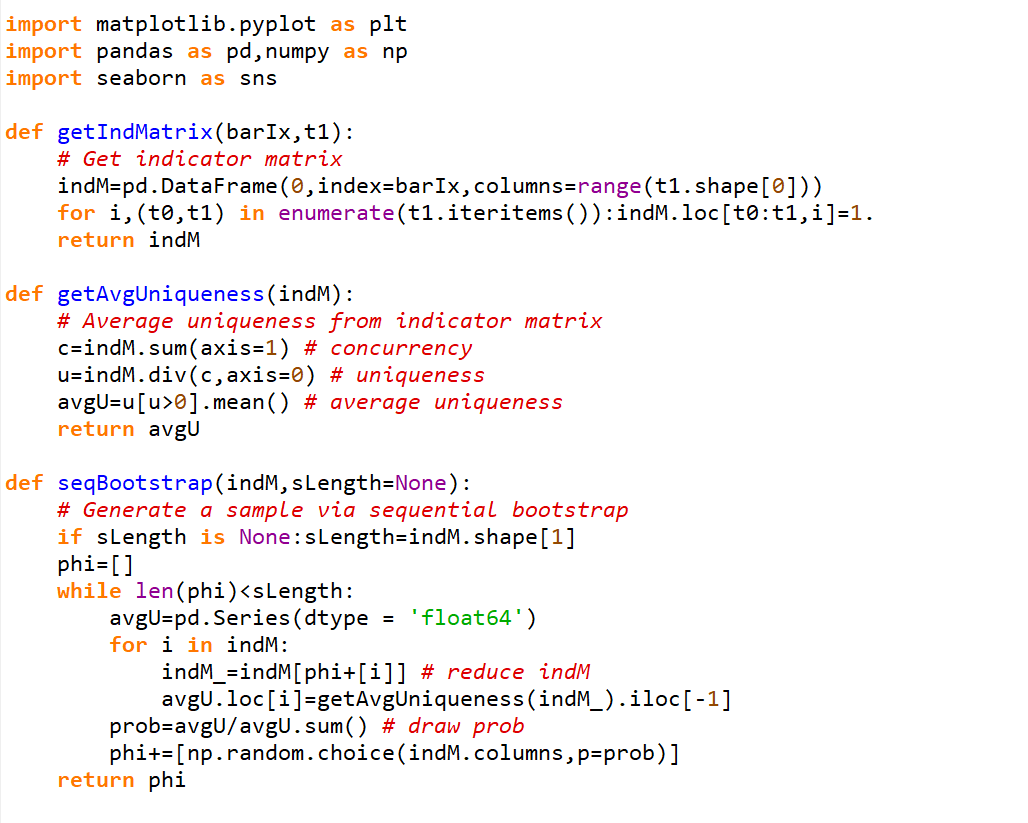
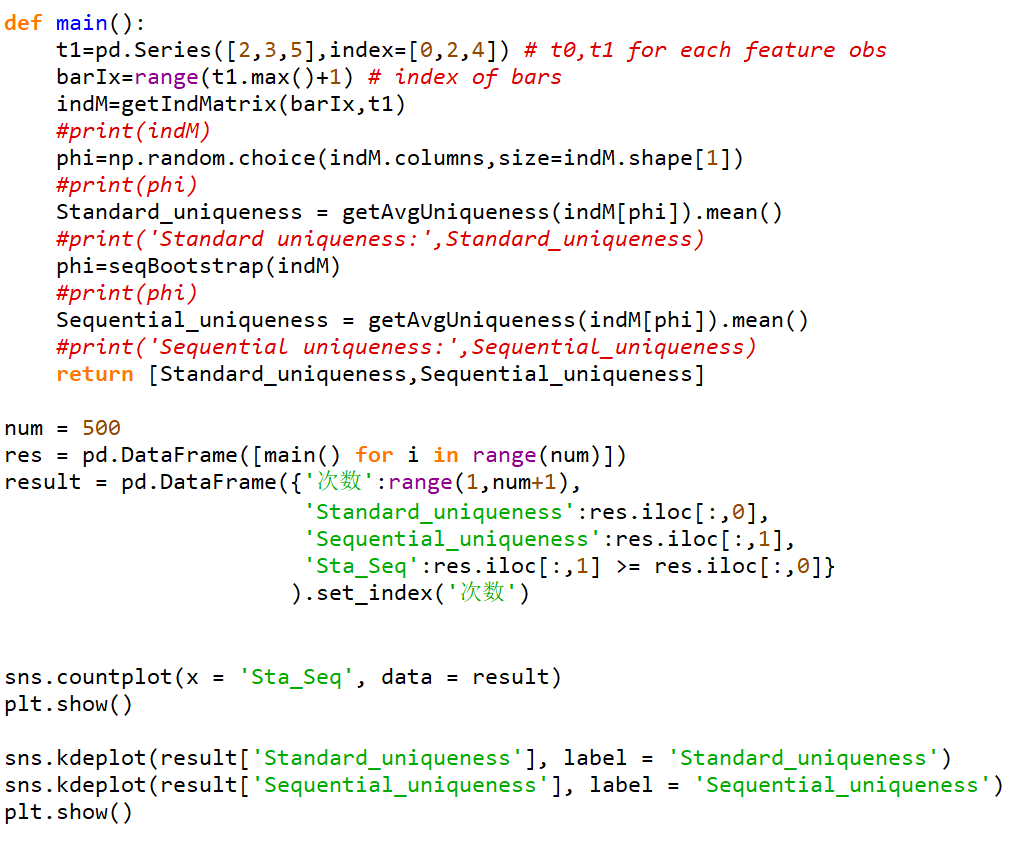
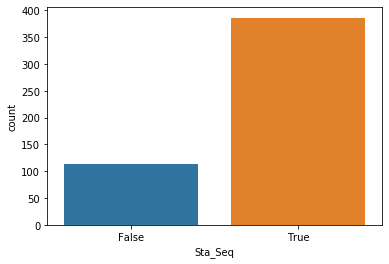
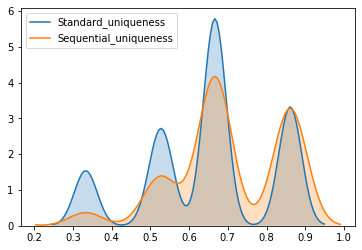
可以看出在500次迭代后，我们可以看出大概80%的Sequential Uniqueness要大于等于Standard Uniqueness。并且根据他们的概率分布图可以看出Sequential Uniqueness的概率分布曲线比Standard Uniqueness更靠右，并且值更多分布在0.7到0.9之间，说明Sequential Boostrap可以更好的避免抽样重复的元素，并能根据uniqueness调节抽样的比率。